
 如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3,EF=4,则边AD的长是( )
如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3,EF=4,则边AD的长是( )| A. | 2 | B. | 3 | C. | 4.8 | D. | 5 |
分析 利用三个角是直角的四边形是矩形易证四边形EFGH为矩形,那么由折叠可得HF的长即为边AD的长.
解答 解:∵∠HEM=∠AEH,∠BEF=∠FEM,
∴∠HEF=∠HEM+∠FEM=$\frac{1}{2}$×180°=90°,
同理可得:∠EHG=∠HGF=∠EFG=90°,
∴四边形EFGH为矩形.
∵AD=AH+HD=HM+MF=HF,HF=$\sqrt{{EH}^{2}+E{F}^{2}}$$\sqrt{{3}^{2}{+4}^{2}}$=5,
∴AD=5,
故选D.
点评 考查学生对翻转、折叠矩形、三角形等知识的掌握情况.错误的主要原因是空间观念以及转化的能力不强,缺乏简单的逻辑推理能力.


科目:初中数学 来源: 题型:解答题
 如图,已知点A(a,3)是一次函数y1=x+b图象与反比例函数y2=$\frac{6}{x}$图象的一个交点.
如图,已知点A(a,3)是一次函数y1=x+b图象与反比例函数y2=$\frac{6}{x}$图象的一个交点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 己知,如图,矩形ABCD中,AD=3,DC=4,矩形EFGH的三个顶点E.G、H分别在矩形ABCD的边ABCD的边AB、CD、DA上,AH=1,连接CF.
己知,如图,矩形ABCD中,AD=3,DC=4,矩形EFGH的三个顶点E.G、H分别在矩形ABCD的边ABCD的边AB、CD、DA上,AH=1,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
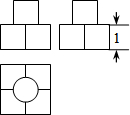 如图是某几何体的三视图,其中主视图和左视图是由若干个大小相等的正方形构成的.根据图中所标的尺寸,该几何体的表面积是16+π(不取近似值).
如图是某几何体的三视图,其中主视图和左视图是由若干个大小相等的正方形构成的.根据图中所标的尺寸,该几何体的表面积是16+π(不取近似值).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A、B(点A在B的左侧),与y轴交于点C,若点F是直线BC上方的抛物线上一动点,是否存在点F,使△BCF的面积最大?若存在,求出定F的坐标;若不存在,请说明理由.
如图,已知抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A、B(点A在B的左侧),与y轴交于点C,若点F是直线BC上方的抛物线上一动点,是否存在点F,使△BCF的面积最大?若存在,求出定F的坐标;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com