
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O. 
(1)证明:四边形ADCE为菱形;
(2)证明:DE=BC.
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
![]()
A.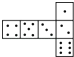 B.
B.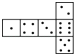 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:
①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.
其中说法正确的有_________(把你认为说法正确的序号都填上).
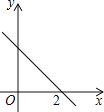
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种水果80千克的钱,现在可买88千克.
(1)现在实际购进这种水果每千克多少元?
(2)王阿姨准备购进这种水果销售,若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系. ①求y与x之间的函数关系式;
②请你帮王阿姨拿个主意,将这种水果的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB上有两点C、D,且AC=BD,M、N分别是线段AC 、AD的中点,若AB=a cm ,AC=BD=b cm,且a,b满足(a-9)2+|b-7 |=0.
![]()
(1)求AB ,AC的长度;
(2)求线段MN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF.经测量,支架的立柱BC与地面垂直,即∠BCA=90°,且BC=1.5m,点F,A,C在同一条水平线上,斜杆AB与水平线AC的夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架的边BE与AB的夹角∠EBD=60°,又测得AD=1m.请你求出该支架的边BE及顶端E到地面的距离EF的长度. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如图①,在△ABC中,试说明∠A+∠B+∠C=180°.
分析:通过画平行线,将∠A、∠B、∠C作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6![]() 的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论:
的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论:
①∠CBH=45°;②点H是EG的中点;③EG=4![]() ;④DG=2
;④DG=2![]() .
.
其中,正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(请用“画树状图”或“列表”等方法写出分析过程);
(2)现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为 ![]() ,求n的值.
,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com