
【题目】判断下列各式从等号左边到右边的变形,哪些是整式乘法,哪些是因式分解.
(1)a2-9b2=(a+3b)(a-3b);
(2)3y(x+2y)=3xy+6y2;
(3)(3a-1)2=9a2-6a+1;
(4)4y2+12y+9=(2y+3)2;
(5)x2+x=x2(1+![]() );
);
(6)x2-y2+4y-4=(x-y)(x+y)+4(y-1).
科目:初中数学 来源: 题型:
【题目】计算:(1)25×26=________;
(2)![]() ×
×![]() =________;
=________;
(3)-a2·a5=________;
(4)x2·x2m-2=________;
(5)(-b)2·(-b)3·(-b)5=________;
(6)x·x4+x5=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).

(1)用的代数式表示PC的长度;
(2)若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
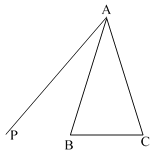
【题目】如图,△ABC中,AB=AC,射线AP在△ABC的外侧,点B关于AP的对称点为D,连接CD交射线AP于点E,连接BE.
(1)根据题意补全图形;
(2)求证:CD=EB+EC;
(3)求证:∠ABE=∠ACE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )

A. 105° B. 110° C. 100° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气象台发现:在某段时间里,如果早晨下雨,那么晚上是晴天;如果晚上下雨,那么早晨是晴天,已知这段时间有9天下了雨,并且有6天晚上是晴天,7天早晨是晴天,则这一段时间有( )
A.9天
B.11天
C.13天
D.22天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.
(1)如图①,若∠BAC=60°,按边分类:△CEF是 ____________ 三角形;
(2)若∠BAC<60°.
①如图②,当点D在线段CB上移动时,判断△CEF的形状并证明;
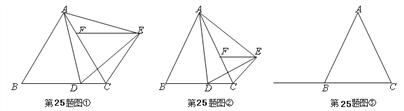
②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请在图③中画出相应的图形,写出结论并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论: ①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )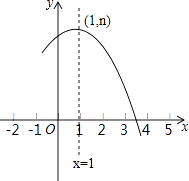
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司保安部去商店购买同一品牌的应急灯和手电筒,查看定价后发现,购买一个应急灯和5个手电筒共需50元,购买3个应急灯和2个手电筒共需85元.
(1)求出该品牌应急灯、手电筒的定价分别是多少元?
(2)经商谈,商店给予该公司购买一个该品牌应急灯赠送一个该品牌手电筒的优惠,如果该公司需要手电筒的个数是应急灯个数的2倍还多8个,且该公司购买应急灯和手电筒的总费用不超过670元,那么该公司最多可购买多少个该品牌应急灯?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com