
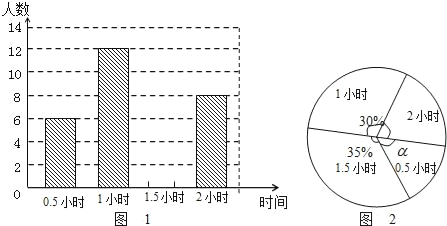
【题目】为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:
(1)本次调查的学生人数是 人;
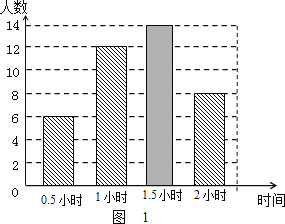
(2)图2中α是 度,并将图1条形统计图补充完整;
(3)请估算该校九年级学生自主学习时间不少于1.5小时有 人;
(4)老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.
【答案】(1)40;(2)54,补图见解析;(3)330;(4)![]() .
.
【解析】
试题(1)根据由自主学习的时间是1小时的人数占30%,可求得本次调查的学生人数;
(2)![]() ,由自主学习的时间是0.5小时的人数为40×35%=14;(3)求出这40名学生自主学习时间不少于1.5小时的百分比乘以600即可;(4)根据题意画出树状图,然后由树状图求得所有等可能的结果与选中小亮A的情况,再利用概率公式求解即可求得答案.
,由自主学习的时间是0.5小时的人数为40×35%=14;(3)求出这40名学生自主学习时间不少于1.5小时的百分比乘以600即可;(4)根据题意画出树状图,然后由树状图求得所有等可能的结果与选中小亮A的情况,再利用概率公式求解即可求得答案.
试题解析:
解:(1)∵自主学习的时间是1小时的有12人,占30%,∴12÷30%=40,故答案为:40; (2分)
(2)![]() ,故答案为:54;自主学习的时间是0.5小时的人数为40×35%=14;补充图形如图:故答案为:54;
,故答案为:54;自主学习的时间是0.5小时的人数为40×35%=14;补充图形如图:故答案为:54;
(3)600×![]() =330; (2分)故答案为:330;
=330; (2分)故答案为:330;
(4)画树状图得:
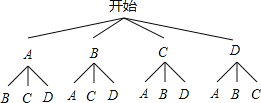
∵共有12种等可能的结果,选中小亮A的有6,
∴P(A)=![]() . (2分)
. (2分)


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(-1,0),B(4,0)C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线![]() 交抛物线于点Q,交直线BD于点M.
交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两张完全相同的矩形纸片![]() 、
、![]() 按如图方式放置,
按如图方式放置,![]() 为重合的对角线.重叠部分为四边形
为重合的对角线.重叠部分为四边形![]() ,
,

![]() 试判断四边形
试判断四边形![]() 为何种特殊的四边形,并说明理由;
为何种特殊的四边形,并说明理由;
![]() 若
若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点![]() ,
,![]() ,
,![]() 三点.
三点.

![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 若点
若点![]() 是线段
是线段![]() 上的点(不与
上的点(不与![]() ,
,![]() 重合),过
重合),过![]() 作
作![]() 轴交抛物线于
轴交抛物线于![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
![]() 在
在![]() 的条件下,连接
的条件下,连接![]() ,
,![]() ,是否存在点
,是否存在点![]() ,使
,使![]() 的面积最大?若存在,求
的面积最大?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,AB=AC,D是射线BC上一点(点D不与点B重合),连结AD,将AD绕着点D逆时针旋转∠BAC的度数得到AE,连结DE、CE.

(1)当点D在边BC上,求证:△BAD≌△CAE.
(2)当点D在边BC上,若∠BAC=a,求∠DCE的大小.(用含a的代数式表示).
(3)当DE与△ABC的边所在的直线垂直,且∠BAC=40°时,请借助图②,直接写出∠CED的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A,B,其顶点为C,如果△ABC是该抛物线的内接格点三角形,AB=3![]() ,且点A,B,C的横坐标xA,xB,xC满足xA<xC<xB,那么符合上述条件的抛物线条数是( )
,且点A,B,C的横坐标xA,xB,xC满足xA<xC<xB,那么符合上述条件的抛物线条数是( )

A. 7 B. 8 C. 14 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为![]() 、
、![]() 、
、![]() ,(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为
,(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为![]() 的圆形区域(只考虑在海平面上的探测).
的圆形区域(只考虑在海平面上的探测).
![]() 若在三艘海监船组成的
若在三艘海监船组成的![]() 区域内没有探测盲点,则雷达的有效探测半径
区域内没有探测盲点,则雷达的有效探测半径![]() 至少为________海里;
至少为________海里;
![]() 某时刻海面上出现一艘菲律宾海警船
某时刻海面上出现一艘菲律宾海警船![]() ,在海监船
,在海监船![]() 测得点
测得点![]() 位于南偏东
位于南偏东![]() 方向上,同时在海监船
方向上,同时在海监船![]() 测得
测得![]() 位于北偏东
位于北偏东![]() 方向上,海警船
方向上,海警船![]() 正以每小时
正以每小时![]() 海里的速度向正西方向移动,我海监船
海里的速度向正西方向移动,我海监船![]() 立刻向北偏东
立刻向北偏东![]() 方向运动进行拦截,问我海监船
方向运动进行拦截,问我海监船![]() 至少以多少速度才能在此方向上拦截到菲律宾海警船
至少以多少速度才能在此方向上拦截到菲律宾海警船![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在7×7网格中,每个小正方形的边长都为1.

(1)若点A(1,3),C(2,1), ①建立适当的平面直角坐标系;②点B的坐标为( , );
(2)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校决定在学生中开设:A、实心球;B、立定跳远;C、跳绳;D、跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图,请结合图中的信息解答下列问题:

(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整.
(3)若调查到喜欢“跳绳”的5名学生中有2名男生,3名女生,现从这5名学生中任意抽取2名学生,请用画树状图或列表法求出刚好抽到不同性别学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com