
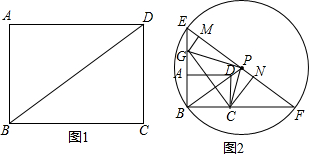
分析 (1)只需分点G在线段AB上(如图①)、在线段AB的延长线上(如图②)、在线段AB的反向延长线上(如图③)三种情况讨论,即可解决问题;
(2)如图2,由(1)可知,此时BG=PG=$\frac{16}{3}$,BC=PC=4.易证△PGM∽△CPN,从而可得PM=$\frac{4}{3}$CN;易证△FNC∽△BCD,从而可得FN=$\frac{4}{3}$CN,即可得到PM=FN.
解答 解:(1)存在点P,使点P、C、G为顶点的三角形与△GCB全等.
①若点G在线段AB上,如图①.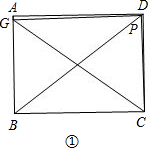
当BG=PC时,根据HL可得Rt△GBC≌Rt△CPG,
此时∠GCB=∠CGP,∠GPC=∠CBG=90°
∴PG∥BC,
∴∠GPC+∠PCB=180°.
∵∠GPC=90°,
∴∠PCB=90°,
∴点P在点D处,
∴BG=PC=DC=AB=3;
②若点G在线段AB的延长线上,如图②.
当BG=PC时,根据HL可得Rt△GBC≌Rt△CPG,
此时BC=PG,∠GCB=∠CGP,
∴OG=OC,OB=OP,
∴∠PBO=∠BPO=$\frac{1}{2}$(180°-∠BOP),
∠OCG=∠OGC=$\frac{1}{2}$(180°-∠GOC).
∵∠BOP=∠GOC,
∴∠PBO=∠OCG,
∴BD∥CG.
∵四边形ABCD是矩形,
∴AB∥DC,即BG∥DC,
∴四边形BGCD是平行四边形,
∴BG=CD=3;
③若点G在线段AB的反向延长线上,如图③.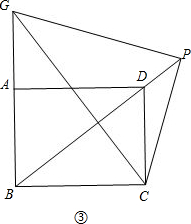
当PC=BC时,根据HL可得Rt△GBC≌Rt△GPC,
此时BG=PG,
∴点G、C在BP的垂直平分线上,
∴GC垂直平分BP,
∴∠BGC+∠GBD=90°.
∵∠CBD+∠GBD=90°,
∴∠BGC=∠CBD.
又∵∠GBC=∠BCD=90°,
∴△GCB∽△BDC,
∴$\frac{BG}{BC}$=$\frac{BC}{CD}$.
∵BC=4,CD=3,
∴$\frac{BG}{4}$=$\frac{4}{3}$,
∴BG=$\frac{16}{3}$;
(2)PM=FN,理由:如图2,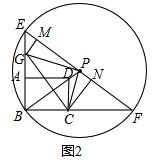
由(1)③可知,此时△GBC≌△GPC,且BG=PG=$\frac{16}{3}$,BC=PC=4.
∵GM⊥EF,CN⊥EF,
∴∠GMP=∠PNC=90°,
∴∠MGP+∠GPM=90°.
∵∠GPC=90°,
∴∠GPM+∠NPC=90°,
∴∠MGP=∠NPC,
∴△PGM∽△CPN,
∴$\frac{PM}{CN}$=$\frac{PG}{CP}$.
∴$\frac{PM}{CN}$=$\frac{\frac{16}{3}}{4}$=$\frac{4}{3}$,即PM=$\frac{4}{3}$CN.
∵PB=PF,
∴∠F=∠PBC.
又∵∠FNC=∠BCD=90°,
∴△FNC∽△BCD,
∴$\frac{FN}{BC}$=$\frac{CN}{DC}$.
∵BC=4,DC=3,
∴$\frac{FN}{4}$=$\frac{CN}{3}$,
∴FN=$\frac{4}{3}$CN,
∴PM=FN.
点评 本题主要考查了矩形的性质、全等三角形的判定与性质、相似三角形的判定与性质、圆的定义、线段垂直平分线性质定理及其逆定理等知识,运用分类讨论的思想是解决第(1)小题的关键,利用相似三角形的性质是解决第(2)小题的关键.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:选择题
| A. | m>1 | B. | m≥1 | C. | m<1 | D. | m≤1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,为测量小区内池塘最宽处A、B两点间的距离,在池塘边定一点C,使∠BAC=90°,并测得AC的长18m,BC的长为30m,则最宽处AB的距离为24m.
如图,为测量小区内池塘最宽处A、B两点间的距离,在池塘边定一点C,使∠BAC=90°,并测得AC的长18m,BC的长为30m,则最宽处AB的距离为24m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,铁路上A,B两点相距20km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=10km,CB=5km,现在要在铁路AB上建一个货运站E,使得C,D两村到E站距离相等,问:E站应建立在离A多少千米处?
如图,铁路上A,B两点相距20km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=10km,CB=5km,现在要在铁路AB上建一个货运站E,使得C,D两村到E站距离相等,问:E站应建立在离A多少千米处?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
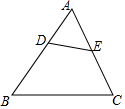 如图所示,D、E分别是△ABC的边AB、AC上的点,试添加一个条件:∠ADE=∠C或∠AED=∠B或$\frac{AD}{AC}=\frac{AE}{AB}$.使得△ABC∽△AED.
如图所示,D、E分别是△ABC的边AB、AC上的点,试添加一个条件:∠ADE=∠C或∠AED=∠B或$\frac{AD}{AC}=\frac{AE}{AB}$.使得△ABC∽△AED.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com