【答案】
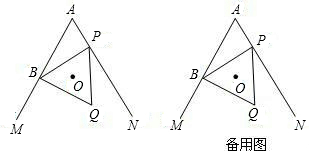
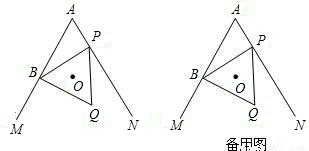
分析:(1)证O在∠MAN的平分线上,可证O到角两边的距离相等,分两种情况:
①OB不与AM垂直,过O作OT⊥AN,OH⊥AM,可通过构建全等三角形来求解.
连接OB,OP,则OB=OP,只需证明△OHB与△OTP全等即可.
这两个三角形中,已知的条件有OB=OP,一组直角.只需再证得一组角对应相等即可,∠HOT和∠BOP都等于120°,因此∠BOH=∠TOP,则两三角形全等,OT=OH.由此得证.
②当OB⊥AM时,由于OB=OP,只需证明OP⊥AN即可.
由于∠BOP=120°,而∠ABO=90°,∠MAN=60°,根据四边形的内角和为360°,即可求得OP⊥AN,由此可得证.
(2)本题要通过相似三角形ACP和ABO来求解.
这两个三角形中,已知了∠BAO=∠CAP(在1题中已经证得).
只需再找出一组对应角相等即可,在△ACP和△OBC中,∠CAP=∠OBC=30°,∠ACP=∠BCO,因此∠APC=∠AOB,由此证得两三角形相似,可得出关于AB,AC,AO,AP的比例关系式,据此可求出y,x的函数关系式.
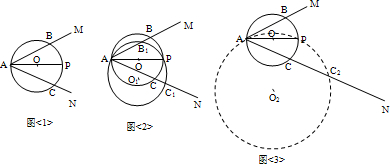
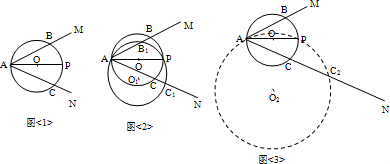
(3)本题分三种情况:
①圆I在△BPQ外,且与BP边相切,此时D、P重合,AD=AP=2,AB=4,∠MAN=60°,因此△ABP为直角三角形,不难得出△ABO也是直角三角形,因此可得出△ABO≌△APB,AO=BP=2
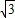
;
②圆I在△BPQ内,与BP,PQ边相切时,此时P与A重合,可在直角三角形ODA中,根据AD=2,∠DAO=30°,求得AO=

;
③圆I在△BPQ内,与BQ边相切时,A,O重合,因此AO=0.
解答: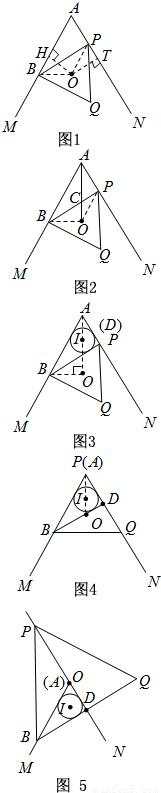
(1)证明:如图1,连接OB,OP.
∵O是等边三角形BPQ的外心,
∴圆心角∠BOP=
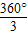
=120°.
当∠MAN=60°,不垂直于AM时,作OT⊥AN,则OB=OP.
由∠HOT+∠A+∠AHO+∠ATO=360°,且∠A=60°,∠AHO=∠ATO=90°,
∴∠HOT=120度.
∴∠BOH=∠POT.
∴Rt△BOH≌Rt△POT.
∴OH=OT.
∴点O在∠MAN的平分线上.
当OB⊥AM时,∠APO=360°-∠A-∠BOP-∠OBA=90°.
即OP⊥AN,
∴点O在圆I的平分线上.
综上所述,当点P在射线AN上运动时,点O在∠MAN的平分线上.
(2)解:如图2,
∵AO平分∠MAN,且∠MAN=60°,
∴∠BAO=∠PAO=30°.
由(1)知,OB=OP,∠BOP=120°,
∴∠CBO=30°,
∴∠CBO=∠PAC.
∵∠BCO=∠PCA,
∴∠AOB=∠APC.
∴△ABO∽△ACP.
∴
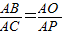
.
∴AC•AO=AB•AP.
∴y=4x.
定义域为:x>0.
(3)解:①如图3,当BP与圆I相切时,AO=2
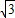
;
②如图4,当BP与圆I相切时,AO=
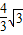
;
③如图5,当BQ与圆I相切时,AO=0.
点评:本题考查了相似三角形、全等三角形、角平分线定理、等边三角形的性质、直线与圆的位置关系等知识点.本题考点较多,难度较大.


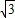 ;
; ;
; (1)证明:如图1,连接OB,OP.
(1)证明:如图1,连接OB,OP.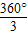 =120°.
=120°.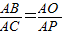 .
.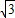 ;
;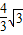 ;
;

 一线名师权威作业本系列答案
一线名师权威作业本系列答案