
【题目】某水产养殖户,一次性收购了![]()
![]() 小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养
小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养![]() 天的总成本为
天的总成本为![]() 万元;放养
万元;放养![]() 天的总成本为
天的总成本为![]() 万元(总成本=放养总费用+收购成本).
万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是![]() 万元,收购成本为
万元,收购成本为![]() 万元,求
万元,求![]() 和
和![]() 的值;
的值;
(2)设这批小龙虾放养![]() 天后的质量为
天后的质量为![]() (
(![]() ),销售单价为
),销售单价为![]() 元/
元/![]() .根据以往经验可知:m与t的函数关系式为
.根据以往经验可知:m与t的函数关系式为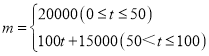 ,y与t的函数关系如图所示
,y与t的函数关系如图所示
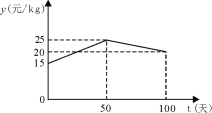
①求y与t的函数关系式;
②设将这批小龙虾放养t天后一次性出售所得利润为W元,求当![]() 为何值时,W最大?并求出W的最大值.(利润=销售总额-总成本)
为何值时,W最大?并求出W的最大值.(利润=销售总额-总成本)
【答案】(1)a的值为0.04,b的值为30;(2)①![]() ;②当t为55天时,w最大,最大值为180250元
;②当t为55天时,w最大,最大值为180250元
【解析】
(1)由放养10天的总成本为30.4万元;放养20天的总成本为30.8万元可得答案;
(2)①分0≤t≤50、50<t≤100两种情况,结合函数图象利用待定系数法求解可得;
②就以上两种情况,根据“利润=销售总额-总成本”列出函数解析式,依据一次函数性质和二次函数性质求得最大值即可得.
解:(1)由题意,得 ![]()
解得![]()
∴![]() 的值为0.04,
的值为0.04,![]() 的值为30
的值为30
(2)①当![]() ≤
≤![]() ≤
≤![]() 时, 设
时, 设![]() 与
与![]() 的函数关系式为
的函数关系式为![]() ,
,
∵![]() 过点(0,15)和(50,25),
过点(0,15)和(50,25),
∴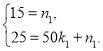
解得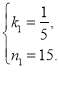
∴![]() 与
与![]() 的函数关系式为
的函数关系式为![]()
当![]() <
<![]() ≤
≤![]() 时, 设
时, 设![]() 与
与![]() 的函数关系式为
的函数关系式为![]()
∵![]() 过点(50,25)和(100,20),
过点(50,25)和(100,20),
∴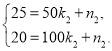
解得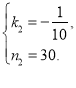
∴![]() 与
与![]() 的函数关系式为
的函数关系式为![]()
∴![]() 与
与![]() 的函数关系式为
的函数关系式为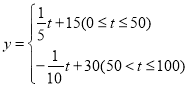
②当![]() ≤
≤![]() ≤
≤![]() 时,
时,![]() .
.
∵3600>0,
∴当![]() 时,
时,![]() 最大值=180000;
最大值=180000;
当![]() <
<![]() ≤
≤![]() 时,
时, ![]()
![]()
∵-10<0,
∴当![]() 时,
时,![]() 最大值=180250.
最大值=180250.
综上所述,当![]() 为
为![]() 天时,
天时,![]() 最大,最大值为180250元.
最大,最大值为180250元.


科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,∠C=90°,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形(不写作法,但须保留作图痕迹).
(2)已知内角度数的两个三角形如图2,图3所示.请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料后,解答问题.分母中含有未知数的不等式叫分式不等式.如:![]() ,
,![]() 等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知,两数相除,同号得正,异号得负,其字母表达式为:
等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知,两数相除,同号得正,异号得负,其字母表达式为:
(1)若![]() ,
,![]() ,则
,则![]() ,若
,若![]() ,
,![]() ,则
,则![]() ;
;
(2)若![]() ,
,![]() ,则
,则![]() ,若
,若![]() ,
,![]() ,则
,则![]() .反之,(1)若
.反之,(1)若![]() ,则
,则![]() 或
或![]()
(3)若![]() ,则__________或_____________.根据上述规律,求不等式
,则__________或_____________.根据上述规律,求不等式![]() ,的解集,方法如下:
,的解集,方法如下:
由上述规律可知,不等式![]() ,转化为①
,转化为①![]() 或②
或②![]()
解不等式组①得![]() ,解不等式组②得
,解不等式组②得![]() .
.
∴不等式![]() ,的解集是
,的解集是![]() 或
或![]() .
.
根据上述材料,解决以下问题:
A、求不等式![]() 的解集
的解集
B、乘法法则与除法法则类似,请你类比上述材料内容,运用乘法法则,解决以下问题:求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种高档蔬菜“莼菜”,其进价为16元/kg.经市场调查发现:该商品的日销售量y(kg)是售价x(元/kg)的一次函数,其售价、日销售量对应值如表:
售价 | 20 | 30 | 40 |
日销售量 | 80 | 60 | 40 |
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围);
的函数解析式(不要求写出自变量的取值范围);
(2)![]() 为多少时,当天的销售利润
为多少时,当天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)由于产量日渐减少,该商品进价提高了![]() 元/
元/![]() ,物价部门规定该商品售价不得超过36元/
,物价部门规定该商品售价不得超过36元/![]() ,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求
,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
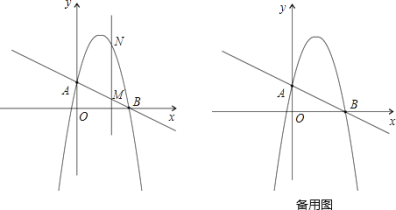
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
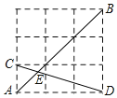
【题目】如图,在由边长为1的小正方形组成的网格中.点 A,B,C,D 都在这些小正方形的格点上,AB、CD 相交于点E,则sin∠AEC的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
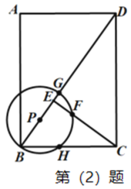
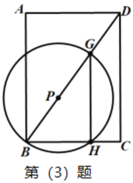
【题目】如图,在矩形 ABCD 中,CE⊥BD,AB=4,BC=3,P 为 BD 上一个动点,以 P 为圆心,PB 长半径作⊙P,⊙P 交 CE、BD、BC 交于 F、G、H(任意两点不重合),
(1)半径 BP 的长度范围为 ;
(2)连接 BF 并延长交 CD 于 K,若 tan KFC 3 ,求 BP;
(3)连接 GH,将劣弧 HG 沿着 HG 翻折交 BD 于点 M,试探究![]() 是否为定值,若是求出该值,若不是,请说明理由.
是否为定值,若是求出该值,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了践行“金山银山,不如绿水青山”的环保理念,重外环保小组的孩子们参与社区公益活动——收集废旧电池,活动开展一个月后,经过统计发现,全组成员平均每人收集了![]() 颗废旧电池,其中,收集数量低于
颗废旧电池,其中,收集数量低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,收集数量不低于
颗,收集数量不低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,数学王老师发现,若每人再多收集
颗,数学王老师发现,若每人再多收集![]() 颗,则收集数量低于
颗,则收集数量低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,收集数量不低于
颗,收集数量不低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,并且,该环保小组的人数介于
颗,并且,该环保小组的人数介于![]() 至
至![]() 人.则该环保小组有__________人.
人.则该环保小组有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L1:y=﹣x2+bx+c经过点A(1,0)和点B(5,0)已知直线l的解析式为y=kx﹣5.
(1)求抛物线L1的解析式、对称轴和顶点坐标.
(2)若直线l将线段AB分成1:3两部分,求k的值;
(3)当k=2时,直线与抛物线交于M、N两点,点P是抛物线位于直线上方的一点,当△PMN面积最大时,求P点坐标,并求面积的最大值.
(4)将抛物线L1在x轴上方的部分沿x轴折叠到x轴下方,将这部分图象与原抛物线剩余的部分组成的新图象记为L2
①直接写出y随x的增大而增大时x的取值范围;
②直接写出直线l与图象L2有四个交点时k的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com