
已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且与x轴交于A、B两点.与y轴交于点C.其中AI(1,0),C(0,
,且与x轴交于A、B两点.与y轴交于点C.其中AI(1,0),C(0,![]() ).
).
(1)(3分)求抛物线的解析式;
(2)若点P在抛物线上运动(点P异于点A).
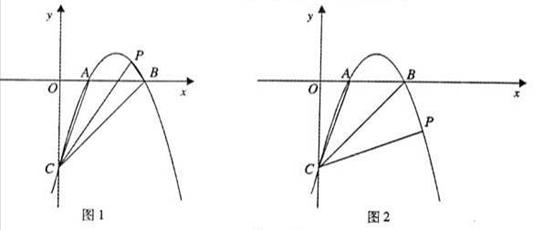
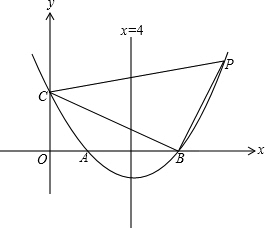
①(4分)如图l.当△PBC面积与△ABC面积相等时.求点P的坐标;
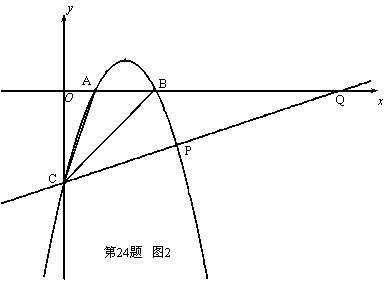
②(5分)如图2.当∠PCB=∠BCA时,求直线CP的解析式。
解:(1)由题意,得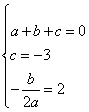 ,解得
,解得
 ∴抛物线的解析式为
∴抛物线的解析式为![]() 。
。
(2)①令![]() ,解得
,解得![]() ∴B(3, 0)
∴B(3, 0)
当点P在x轴上方时,如图1,
过点A作直线BC的平行线交抛物线于点P,
易求直线BC的解析式为![]() ,
,
∴设直线AP的解析式为![]() ,
,
∵直线AP过点A(1,0),代入求得![]() 。
。
∴直线AP的解析式为![]()
解方程组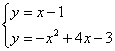 ,得
,得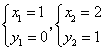
∴点![]()
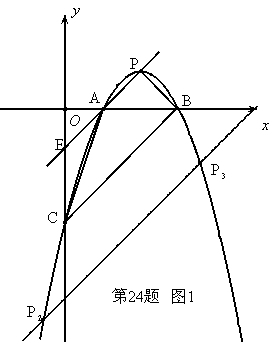
当点P在x轴下方时,如图1
设直线![]() 交y轴于点
交y轴于点![]() ,
,
把直线BC向下平移2个单位,交抛物线于点![]() ,
,
得直线![]() 的解析式为
的解析式为![]() ,
,
解方程组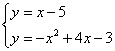 ,得
,得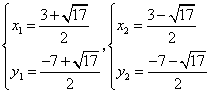
∴![]()
综上所述,点P的坐标为:![]() ,
,![]()
 ②∵
②∵![]()
∴OB=OC,∴∠OCB=∠OBC=45°
设直线CP的解析式为![]()
如图2,延长CP交x轴于点Q,
设∠OCA=α,则∠ACB=45°![]() α
α
∵∠PCB=∠BCA ∴∠PCB=45°![]() α
α
∴∠OQC=∠OBC-∠PCB=45°-(45°![]() α)=α
α)=α
∴∠OCA=∠OQC
又∵∠AOC=∠COQ=90°
∴Rt△AOC∽Rt△COQ
∴![]() ,∴
,∴![]() ,∴OQ=9,∴
,∴OQ=9,∴![]()
∵直线CP过点![]() ,∴
,∴![]()
∴![]()
∴直线CP的解析式为![]() 。
。
其它方法略。


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
 线x=-1,其中B(1,0),C(0,-3).
线x=-1,其中B(1,0),C(0,-3).查看答案和解析>>
科目:初中数学 来源: 题型:
 点,与y轴交于C点,且A、C坐标为(2,0)、(0,3).
点,与y轴交于C点,且A、C坐标为(2,0)、(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•澄江县一模)如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C,已知抛物线的对称轴为x=1.
(2013•澄江县一模)如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C,已知抛物线的对称轴为x=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com