
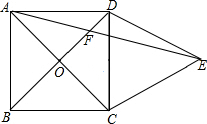
 如图,正方形ABCD,△DCE是等边三角形,AC、BD交于点O,AE交BD于点F.
如图,正方形ABCD,△DCE是等边三角形,AC、BD交于点O,AE交BD于点F.分析 (1)先根据正方形和等边三角形的性质证明△ADE是等腰三角形,即可求出∠DAE=∠DEA.
(2)求出∠OAF=30°,在RT△OAF中利用30度角性质,即可解决问题.
解答 解:(1)∵四边形ABCD是正方形,△CDE是等边三角形,
∴AD=CD,∠ADC=90°,DC=DE,∠CDE=∠DEC=60°,∠DAC=45°,AC⊥BD,
∴AD=DE,∠ADE=90°+60°=150°,∠AOD=90°,
∴∠DAE=∠DEA=$\frac{1}{2}$(180°-150°)=15°,
∴∠AED=15°.
(2)由(1)可知∠OAF=45°-15°=30°,
∴AF=2OF,
∵OF=1,
∴AF=2,AO=$\sqrt{A{F}^{2}-O{F}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴AO=OB=$\sqrt{3}$,
在RT△AOB中,∵∠AOB=90°,∴AB=$\sqrt{A{O}^{2}+O{B}^{2}}$=$\sqrt{6}$.
点评 本题考查了正方形的性质和等边三角形的性质、含30°角的直角三角形的性质以及等腰三角形的判定方法;根据正方形和等边三角形的性质弄清各个角之间的关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
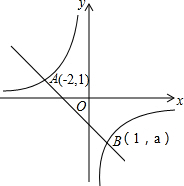 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{a}{x}$的图象相交于A、B两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{a}{x}$的图象相交于A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
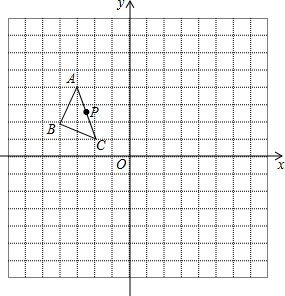 如图,△ABC三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1).
如图,△ABC三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
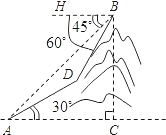 如图,我校九年级一个学习小组进行测量小山高度的实践活动,部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60°,请你帮助他们计算出小山BC的高度(结果保留根号).
如图,我校九年级一个学习小组进行测量小山高度的实践活动,部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60°,请你帮助他们计算出小山BC的高度(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com