
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,点
两点,点![]() 在以
在以![]() 为圆心,1为半径的
为圆心,1为半径的![]() 上,
上,![]() 是
是![]() 的中点,已知
的中点,已知![]() 长的最小值为1,则
长的最小值为1,则![]() 的值为______.
的值为______.

【答案】![]()
【解析】
作辅助线,先确定OM长的最大时,点P的位置,当BP过圆心C时,设B(t,-3t),则CD=3-t,BD=-3t,根据勾股定理计算t的值,可得k的值.

如图,连接BP,由对称性得:OA=OB,
∵M是AP的中点,
∴OM=![]() BP,
BP,
∵OM长是最小值为1,
∴BP长的最小值为1×2=2,
如图,当BP过圆点C时,BP最长,过B作BD⊥x轴于D,
∵CP=1,∴BC=BP+CP=3,
∵B在直线y=-2x上,设B(t,-3t),则CD=3-t,BD=-3t,
在Rt△BCD中,由勾股定理得:
BC2=CD2+BD2,
∴32=(3-t)2+(-3t)2,解得t=0(舍)或![]() ,
,
∴B(![]() ,
,![]() ),
),
∵点B在反比例函数![]() 的图象上,
的图象上,
∴k=![]() ×
×![]() =
=![]() .
.
故答案为: ![]() .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
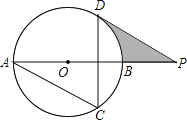
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+6与x轴交于点A(6,0),B(﹣1,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)若点M为该抛物线对称轴上一点,当CM+BM最小时,求点M的坐标.
(3)抛物线上是否存在点P,使△BCP为等腰三角形?若存在,有几个?并请在图中画出所有符合条件的点P,(保留作图痕迹);若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个三角形先沿x轴翻折,再向右平移两个单位称为一次变换,如图,已知等边三角形ABC的顶点B、C的坐标分别是,(-1,-1),(-3,-1),把三角形ABC经过连续9次这样的变换得到三角形A’B’C’,则点A的对应点A’的坐标是_____
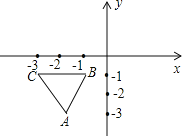
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC顶点A(6,0)、C(0,4),直线![]() 分别交BA、OA于点D、E,且D为BA中点。
分别交BA、OA于点D、E,且D为BA中点。
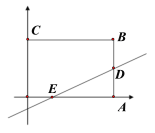
(1)求k的值及此时△EAD的面积;
(2)现向矩形内随机投飞镖,求飞镖落在△EAD内的概率。(若投在边框上则重投)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() ,
,![]() .
.
(1)求该抛物线的函数表达式及对称轴;
(2)设点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 是抛物线对称轴上一动点,记抛物线在
是抛物线对称轴上一动点,记抛物线在![]() ,
,![]() 之间的部分为图象
之间的部分为图象![]() (包含
(包含![]() ,
,![]() 两点),如果直线
两点),如果直线![]() 与图象
与图象![]() 有一个公共点,结合函数的图象,直接写出点
有一个公共点,结合函数的图象,直接写出点![]() 纵坐标
纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
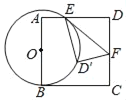
【题目】如图,O是正方形ABCD边上一点,以O为圆心,OB为半径画圆与AD交于点E,过点E作⊙O的切线交CD于F,将△DEF沿EF对折,点D的对称点D'恰好落在⊙O上.若AB=6,则OB的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com