
【题目】如图,在⊙O中,B,P,A,C是圆上的点,PB= PC, PD⊥CD,CD交⊙O于A,若AC=AD,PD =![]() ,sin∠PAD =
,sin∠PAD =![]() ,则△PAB的面积为_______.
,则△PAB的面积为_______.
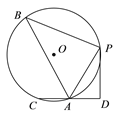
【答案】2
【解析】分析: 连接PC PB PA,过P做BA垂线于H点,根据PB=PC,再由全等三角形的判定定理可得出△PBH≌△PCD,Rt△PHA≌Rt△PDA,根据AC=AD=1即可得出结论.
详解: 连接PC PB PA,过P做BA垂线于H点,
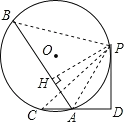
∵PD⊥CD, PD =![]() ,sin∠PAD =
,sin∠PAD =![]() ,
,
∴AP=![]() ,AD=1,
,AD=1,
∵AC=AD,
∴CD=2.
在△PBH与△PCD中,
∠B=∠C
PB=PC
∠BPH=∠DPC,
∴△PBH≌△PCD(ASA),
∴BH=CD=2,PH=PD=![]() ,
,
∴AH=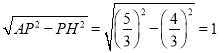 ,
,
∴△PAB的面积为AB×PH×![]() =(2+1)×
=(2+1)×![]() ×
×![]() =2,
=2,
故答案为:2.
点睛:
本题考查的是圆周角定理及全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知A、B、C三点在数轴上的位置如图所示,它们表示的数分别是a、b、c
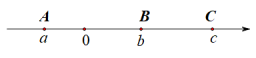
(1) 填空:abc________0,a+b________ac,ab-ac________0;(填“>”,“=”或“<”)
(2) 若|a|=2,且点B到点A、C的距离相等
① 当b2=16时,求c的值
② 求b、c之间的数量关系
③ P是数轴上B,C两点之间的一个动点设点P表示的数为x.当P点在运动过程中,bx+cx+|x-c|-10|x+a|的值保持不变,求b的值
查看答案和解析>>
科目:初中数学 来源: 题型:
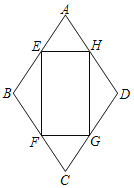
【题目】如图,菱形ABCD中,AB=1,∠A=60°,EFGH是矩形,矩形的顶点都在菱形的边上.设AE=AH=x(0<x<1),矩形的面积为S.
(1)求S关于x的函数解析式;
(2)当EFGH是正方形时,求S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
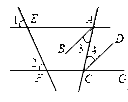
证明:∵ ∠1="∠2" ( 已知 )
∴ AE∥ ( )
∴ ∠EAC =∠ ,( )
而AB平分∠EAC,CD平分∠ACG( 已知 )
∴∠ =![]() ∠EAC,∠4=
∠EAC,∠4=![]() ∠ ( 角平分线的定义 )
∠ ( 角平分线的定义 )
∴∠ =∠4(等量代换)
∴AB∥CD( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解):A,B,C为数轴上三点,若点C到A的距离CA是点C到B的距离CB的2倍,我们就称点C是(A,B)的好点.例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离CA是2,到点B的距离CB是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离DA是1,到点B的距离DB是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
(知识运用):(1)如图1,表示数______和_______的点是(A,B)的好点;

(2)如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.

①表示数______的点是(M,N)的好点;
②表示数______的点是(N,M)的好点;
(3)如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动.当t为何值时,P、A和B中恰有一个点为其余两点的好点?
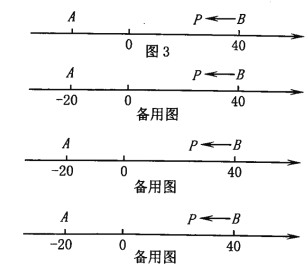
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某图书馆计划选购甲、乙两种图书.甲图书每本价格是乙图书每本价格的2.5倍,如果用900元购买图书,则单独购买甲图书比单独购买乙图书要少18本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本,且用于购买甲、乙两种图书的总费用不超过1725元,那么该图书馆最多可以购买多少本乙图书?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com