
【题目】如图,已知梯形ABCD中,AD∥BC,AB=CD=AD,AC、BD相交于点O,∠BCD=60°,则下列4个结论:①梯形ABCD是轴对称图形;②BC=2AD;③梯形ABCD是中心对称图形;④AC平分∠DCB,其中正确的是_____.
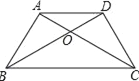
【答案】①②④
【解析】
根据等腰梯形的性质即可求出答案.
①∵AB=CD,
∴梯形ABCD是等腰梯形,
∴过点O作直线l⊥BC,此时直线l为梯形的对角线,故①正确;
②如图,过点D作DE∥AB,
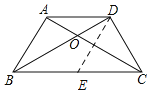
易证,四边形ADEB是平行四边形,
∴AD=BE,AB=DE,
∵AB=CD,
∴DE=CD,
∵∠BCD=60°,
∴△DEC是等边三角形,
∴CE=CD,
∴BC=BE+CE=AD+CD=2AD,故②正确;
③根据中心对称图形的定义可知等腰梯形ABCD不是中心对称图形,故③错误;
④∵AD=CD,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DCA=∠ACB,
∴CA平分∠DCB,故④正确;
故答案为:①②④


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 是
是![]() 的内心,过点
的内心,过点![]() 作
作![]() ,与
,与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,则( )
,则( )
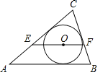
A. EF>AE+CF B. EF<AE+CF C. EF=AE+BF D. EF≤AE+CF
查看答案和解析>>
科目:初中数学 来源: 题型:
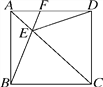
【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场销售一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下.若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(2)每千克水果涨价多少元时,商场每天获得的利润最大?获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
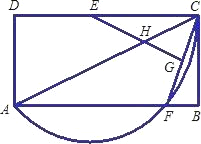
【题目】已知:如图,矩形ABCD中,点E、F分别在DC,AB边上,且点A、F、C在以点E为圆心,EC为半径的圆上,连接CF,作EG⊥CF于G,交AC于H.已知AB=6,设BC=x,AF=y.
(1)求证:∠CAB=∠CEG;
(2)①求y与x之间的函数关系式. ②x= 时,点F是AB的中点;
(3)当x为何值时,点F是![]() 的中点,以A、E、C、F为顶点的四边形是何种特殊四边形?试说明理由.
的中点,以A、E、C、F为顶点的四边形是何种特殊四边形?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程x2﹣4x=12;
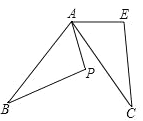
(2)如图,△ABP是由△ACE绕A点旋转得到的,若∠APB=110°,∠B=30°,∠PAC=20°,求旋转角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP∶BC=2∶3.其中能推出△ABP∽△ECP的有( )
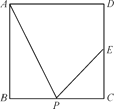
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com