
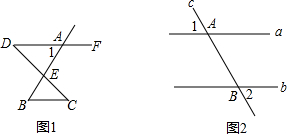
分析 A.两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角,据此进行判断即可.
B.根据平行线的性质以及对顶角相等,即可得到∠2的度数.
解答 解:若选A,
根据DF,BC被AB所截,可得∠1与∠B是内错角;
根据DF,DC被AE所截,可得∠1与∠AEC是内错角;
故答案为:∠B和∠AEC;
若选B,
如图2,∵直线a∥b,
∴∠1=∠3=70°,
∴∠2=∠3=70°,
故答案为:70°.
点评 本题主要考查了内错角的概念以及平行线的性质的运用,解题时注意:两直线平行,同位角相等;同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形..


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
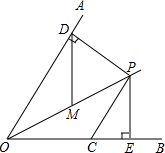 如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是$\sqrt{3}$.
如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O的弦AB、CD交于点E,点A是$\widehat{CD}$的中点,连接AC、BC,延长DC到点P,连接PB.
如图,⊙O的弦AB、CD交于点E,点A是$\widehat{CD}$的中点,连接AC、BC,延长DC到点P,连接PB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:
荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com