
【题目】已知四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
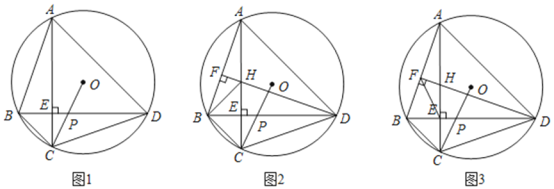
(1)如图1,求证:![]() ;
;
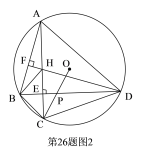
(2)如图2,作![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 长.
长.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)延长CO交⊙O于K,连接DK,利用圆周角定理得到∠CDK=90°,根据AC⊥BD及圆周角定理求得∠CBD=∠CKD,即可求出结论;
(2)根据垂直的定义及圆周角定理得到∠BDC=∠BDF,得到DB垂直平分CH,即可证得结论;
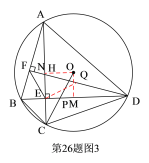
(3)作EQ⊥EF交FD于Q,ON⊥AC于N,OM⊥BD于M ,先证△AED与△BEC都为等腰直角三角形,根据 △AEF≌△DEQ求出![]() ,勾股定理得AD=
,勾股定理得AD=![]() ,得到AE=ED=12,再利用BE:DE=1:3及勾股定理求出OC即可.
,得到AE=ED=12,再利用BE:DE=1:3及勾股定理求出OC即可.
(1)解:延长CO交⊙O于K,连接DK.
∵CK为⊙O直径,
∴∠CDK=90°,
∴∠OCD+∠CKD=90°,
∵AC⊥BD于E ,
∴∠BEC=90°,
∴∠ACB+∠CBD=90°,
∵∠CBD=∠CKD,
∴∠ACB=∠OCD ;

(2)∵DF⊥AB于F,
∴∠DFB=90°,
∵AC⊥BD于E,
∴∠AEB=90°,
∴∠BAC+∠DBF=90°,
∴∠BDF+∠DBF=90°,
∴∠BDF=∠BAC,
∵∠BAC=∠BDC,
∴∠BDC=∠BDF,
∴∠DHC=∠DCH,
∴DB垂直平分CH,
∴BH=BC;
(3)作EQ⊥EF交FD于Q,ON⊥AC于N,OM⊥BD于M ,
∵BC∥AD,
∴∠BCA=∠DAC,
∵∠BCA=∠ADB,
∴∠DAC=∠ADB,
∴△AED与△BEC都为等腰直角三角形,
∵△AEF≌△DEQ,
∴AF=QD=![]() ,EF=EQ=
,EF=EQ=![]() ,
,
∴FQ=![]() ,
,
∴![]() ,勾股定理得AD=
,勾股定理得AD=![]() ,
,
∴AE=ED=12,
∵BE:DE=1:3,
∴BE=CE=4,
∴BD=AC=16,
∴BM=CN=8,
∴OM=EN=4,
∴ON=EM=4,
∴OC=![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,A的坐标为(0,0),B的坐标为(﹣3,1).
(1)将线段AB绕点A逆时钟旋转θ度(0<θ<180),得到对应的线段AE,当AE∥CD时,设在此过程中线段AB所扫过的区域面积为S,点B所经过的路径长为l,则S= ;l= .
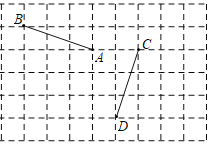
(2)是否存在点P,使得线段AB可由线段CD绕点P旋转一个角度而得到?若存在,直接写出点P的坐标(写出一个即可);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
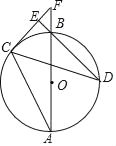
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.
(1)求证:CF是⊙O的切线;
(2)当BD=![]() ,sinF=
,sinF=![]() 时,求OF的长.
时,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在近期“抗疫”期间,某药店销售A、B两种型号的口罩,已知销售800只A型和450只B型的利润为210元,销售400只A型和600只B型的利润为180元.
(1)求每只A型口罩和B型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不超过A型口罩的3倍,设购进A型口罩x只,这2000只口罩的销售总利润为y元.
①求y关于x的函数关系式;
②该药店购进A型、B型口罩各多少只,才能使销售总利润最大?
(3)在销售时,该药店开始时将B型口罩提价100%,当收回成本后,为了让利给消费者,决定把B型口罩的售价调整为进价的15%,求B型口罩降价的幅度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15![]() .(sin15°=0.259,cos15°=0.966,tan15°=0.268,结果精确到0.1m)
.(sin15°=0.259,cos15°=0.966,tan15°=0.268,结果精确到0.1m)
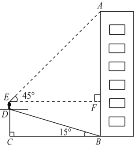
(1)求李华此时与地面的垂直距离CD的值;
(2)李华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45![]() ,求楼房AB的高度.
,求楼房AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求本次比赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+bx+c经过原点,且当x=2时函数有最小值;直线AC解析式为y=kx-4,且与抛物线相交于B、C.
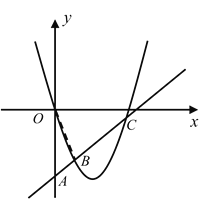
(1)求二次函数解析式;
(2)若S△AOB∶S△BOC=1:3,求直线AC的解析式;
(3)在(2)的条件下,点E为线段BC上一动点(不与B、C重合),过E作x轴的垂线交抛物线于F、交x轴于G,是否存在点E,使△BEF和△CGE相似?若存在,请求出所有点E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com