
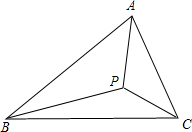
如图P是△ABC所在平面上一点.如果∠APB=∠B![]() PC=∠CPA=120°,则点P就叫做费马点.
PC=∠CPA=120°,则点P就叫做费马点.
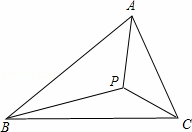
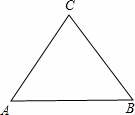
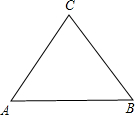
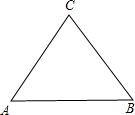
(1)当△ABC是等边三角形时,作尺规法作出△ABC费马点.(不要求写出作法,只要保留作图痕迹)
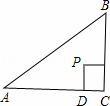
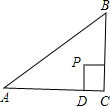
(2)已知:△ABC是等腰直角三角形,∠C=90°,AC=BC=![]() .四边形CDPE是正方形,CD在AC上,CE在BC上,P是△ABC的费马点.求:P点到AB的距离.
.四边形CDPE是正方形,CD在AC上,CE在BC上,P是△ABC的费马点.求:P点到AB的距离.
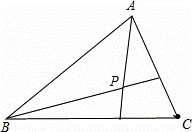
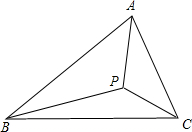
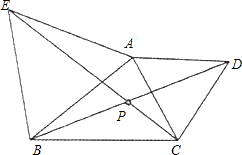
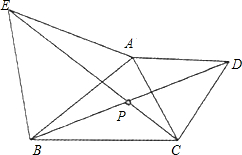
(3)已知:锐角△ABC,分别以AB,AC为边向外作正△ABE和正△ACD,CE和BD相交于P点.
①求∠CPD的度数;
②求证:P点为△ABC的费马点.

解:(1)△ABC费马点如图所示:
(2)连接AP,BP,CP并延长交AB于Q点.
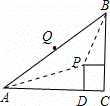
∵P是△ABC费马点,
∴∠APC=∠BOC=120°.
∵四边形CDPE是正方形,
∴∠PCD=∠PCE=45°.
∵CP=CP,
∴△ACP≌△DCP.
∴AP=BP.
∴CQ⊥AB.
∵∠APC=120°,
∴∠APQ=60°.
∴PQ=AQ3.
∵△ABC是等腰直角三角形,
∴AB=2AC=2×6=23.
AQ=AB2=3,
∴PQ=33=1.
(3)①∵△ACE≌△ABD,
∵∠1=∠2,
∵∠3=∠4,
∵∠CPD=∠5=60°. ②∵△ADF∽△CFP,
∴AFPF=DFCF.
∵∠![]() AFP=∠CFD,
AFP=∠CFD,
∴△AFP∽△CDF.
∴∠APF=∠ACD=60°.
∴∠APC=∠CPD+∠APF=120°.
∴∠BPC=120°.
∴∠APB=360°-![]() ∠
∠![]() BPC-∠APC=
BPC-∠APC=![]() 120°.
120°.
∴P点为△ABC的费马点.


科目:初中数学 来源: 题型:
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 .四边形CDPE是正方形,CD在AC上,CE在BC上,P是△ABC的费马点.求:P点到AB的距离.
.四边形CDPE是正方形,CD在AC上,CE在BC上,P是△ABC的费马点.求:P点到AB的距离.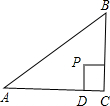
查看答案和解析>>
科目:初中数学 来源: 题型:
如图:
(1)根据△ABC所在位置,写出A、B、C三点的坐标;
(2)将△ABC向左平移6个单位?再向上平移5个单位,则平移后各个顶点的坐标是多少?在图中画出平移后的图形.

查看答案和解析>>
科目:初中数学 来源:2010年浙江省宁波市鄞州区中考数学模拟试卷(解析版) 题型:解答题


 .四边形CDPE是正方形,CD在AC上,CE在BC上,P是△ABC的费马点.求:P点到AB的距离.
.四边形CDPE是正方形,CD在AC上,CE在BC上,P是△ABC的费马点.求:P点到AB的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com