
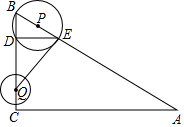
 ��ͼ���ڡ�ABC�У���ACBΪֱ�ǣ�AB=10����A=30�㣬�뾶Ϊ1�Ķ�ԲQ��Բ�Ĵӵ�C����������CB������1����λ����/����ٶ������˶���ͬʱ����P�ӵ�B����������BA����Ҳ��1����λ����/����ٶ������˶������˶�ʱ��Ϊt�루0��t��5����PΪԲ�ģ�PB��Ϊ�뾶�ġ�P��AB��BC����һ������ֱ�ΪE��D������ED��EQ��
��ͼ���ڡ�ABC�У���ACBΪֱ�ǣ�AB=10����A=30�㣬�뾶Ϊ1�Ķ�ԲQ��Բ�Ĵӵ�C����������CB������1����λ����/����ٶ������˶���ͬʱ����P�ӵ�B����������BA����Ҳ��1����λ����/����ٶ������˶������˶�ʱ��Ϊt�루0��t��5����PΪԲ�ģ�PB��Ϊ�뾶�ġ�P��AB��BC����һ������ֱ�ΪE��D������ED��EQ������ ��1������ֱ�����Ե�Բ�ܽ���ֱ�ǣ���֪��BDE=��BCA=90�㣬�ɴ˼���֤����
��2����ͼ3�У����P��AC�ཻ��M��N��BP=CQ=t��AP=AB-BP=10-t������P��PH��AC��H����Rt��APH�У��ɡ�A=30�㣬�Ƴ�PH=$\frac{1}{2}$AP=$\frac{1}{2}$��10-t������Rt��PHN�У�NH=$\sqrt{P{N}^{2}-P{H}^{2}}$=$\frac{1}{2}$$\sqrt{3{t}^{2}+20t-100}$���Ƴ�MN=2MH=$\sqrt{3{t}^{2}+20t-100}$����y=$\sqrt{3{t}^{2}+20t-100}$���ɴ˼��ɽ����⣮
��3������P���Q����ʱ����ͼ4�У���PH��BC��H����֪��ʱ��QBP=60�㣬BQ=5-t��PQ=t+1��BP=t����Rt��PHQ�У����ù��ɶ��������г����̽�����⣮
��� �⣺��1�����ۣ�DE��BC���������£�
��ͼ1�У�
��BE��ֱ����
���BDE=90�㣬
��DE��BC��
�ߡ�BCA=90�㣬��A=30�㣬
��DE��AC��
���BDE�ס�BCA��
��$\frac{BD}{BE}$=$\frac{BC}{BA}$=$\frac{1}{2}$��
��ͼ2�У���C��D�غ�ʱ����CQ=CD=t����BD=5-t��BE=2t��
��$\frac{5-t}{2t}$=$\frac{1}{2}$��
��t=$\frac{5}{2}$��
�൱t=$\frac{5}{2}$ʱ��Q��D�غϣ�
��2����ͼ3�У����P��AC�ཻ��M��N��BP=CQ=t��AP=AB-BP=10-t��
����P��PH��AC��H��
��Rt��APH�У��ߡ�A=30�㣬
��PH=$\frac{1}{2}$AP=$\frac{1}{2}$��10-t����
��Rt��PHN��NH=$\sqrt{P{N}^{2}-P{H}^{2}}$=$\frac{1}{2}$$\sqrt{3{t}^{2}+20t-100}$��
MN=2MH=$\sqrt{3{t}^{2}+20t-100}$��
��y=$\sqrt{3{t}^{2}+20t-100}$��
����O������B��ʱ��CQ=CB-QB=4��
��t=$\frac{4}{1}$����õ���MN=2$\sqrt{7}$��
��3������P���Q����ʱ����ͼ4�У���PH��BC��H����֪��ʱ��QBP=60�㣬BQ=5-t��PQ=t+1��BP=t��
����Rt��PBH��BH=$\frac{1}{2}$PB=$\frac{1}{2}$t��PH=$\frac{\sqrt{3}}{2}$t��
��Rt��PHQ��PH2+QH2=PQ2��
�ࣨ$\frac{\sqrt{3}}{2}$t��2+��5-$\frac{3}{2}$t��2=��t+1��2��
������2t2-17t+24=0��
���t=$\frac{17-\sqrt{97}}{4}$��$\frac{17+\sqrt{97}}{4}$��������
�ߴӴ�ʱ��ֹͣ�˶�����P���Q�������ཻλ�ã�
���P���Q�ཻʱ��t��ȡֵ��ΧΪ$\frac{17-\sqrt{97}}{4}$��t��5��
���� ���⿼��Բ�ۺ��⡢���ɶ�����ƽ���ߵ����ʡ����������ε��ж������ʡ���Բ���е����ʡ����ɶ�����֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�ѧ���ù������̵�˼��˼�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -m8n4 | B�� | mn4 | C�� | -m9n | D�� | 5m3n2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ�ø�Ϊ8m�Ĵ�����̨��ζϣ������������3m��C���۶ϣ������������������ײ�������������
��ͼ��һ�ø�Ϊ8m�Ĵ�����̨��ζϣ������������3m��C���۶ϣ������������������ײ�������������| A�� | 4m | B�� | 5m | C�� | 6m | D�� | 7m |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
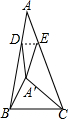 ��ͼ���ڡ�ABC�У�AB=AC����A=30�㣬BC=$\sqrt{6}$����D��AB�ϵ�һ�㣬��AD=$\sqrt{3}$��BD=3������A�ع�D���ֱ��DE���ۣ���A����A���λ�ã�����BA�䡢A��C��������A��BC�ǵ��������Σ����BA��D=120���180���90�㣮
��ͼ���ڡ�ABC�У�AB=AC����A=30�㣬BC=$\sqrt{6}$����D��AB�ϵ�һ�㣬��AD=$\sqrt{3}$��BD=3������A�ع�D���ֱ��DE���ۣ���A����A���λ�ã�����BA�䡢A��C��������A��BC�ǵ��������Σ����BA��D=120���180���90�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
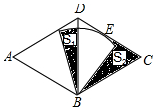 ��ͼ������ABCD����A=60�㣬AB=4���Ե�BΪԲ�ĵ��������CD�����ڵ�E�����ε�Բ�Ľ�Ϊ60�㣬��E��CD���е㣬ͼ��������Ӱ���ֵ�����ֱ�ΪS1��S2����S2-S1=2$\sqrt{3}$-�У�
��ͼ������ABCD����A=60�㣬AB=4���Ե�BΪԲ�ĵ��������CD�����ڵ�E�����ε�Բ�Ľ�Ϊ60�㣬��E��CD���е㣬ͼ��������Ӱ���ֵ�����ֱ�ΪS1��S2����S2-S1=2$\sqrt{3}$-�У��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com