
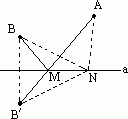
如图所示,在公路a的同旁有两个仓库A、B.现需要建一货物中转站,要求到A、B两仓库的距离和最短,这个中转站M应建在公路旁的哪个位置比较合理?
|
解:已知:直线a和直线同侧两点A、B,如图中所示. 求作:点M,使点M在直线a上,并且AM+BM最小 作法:(1)作B点关于直线a的对称点 (2)连结 理由:在直线a上任取一点N,连结AN、BN、 因为B、 在△A 说明:本题是关于利用对称轴选择最佳位置问题,有助于培养学生运用所学知识分析、解决实际问题的能力. |
|
提示:若A、B两点在直线a的异侧,我们能很自然地想到连接AB,交点即为所求作的点. 但因为本题中A、B两点位于直线a的同侧,如何将之转化为异侧呢?我们易联想到全等三角形之中的“翻折” |


科目:初中数学 来源: 题型:
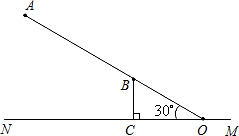 ,直线AB与公路MN的夹角∠AON=30°,新开发区B到公路MN的距离BC=3千米.
,直线AB与公路MN的夹角∠AON=30°,新开发区B到公路MN的距离BC=3千米.查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com