
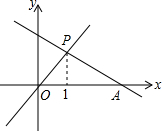
 如图,已知一次函数y=kx+b(k,b为常数,且k≠0)的图象与x轴相交于点A(3,0),若正比例函数y=mx(m为常数,且m≠0)的图象与一次函数的图象相交于点P,且点P的横坐标为1,则关于x的不等式(k-m)x+b>0的解集为x<1,关于x的不等式组$\left\{\begin{array}{l}{mx<0}\\{kx-b<0}\end{array}\right.$的解集为-3<x<0.
如图,已知一次函数y=kx+b(k,b为常数,且k≠0)的图象与x轴相交于点A(3,0),若正比例函数y=mx(m为常数,且m≠0)的图象与一次函数的图象相交于点P,且点P的横坐标为1,则关于x的不等式(k-m)x+b>0的解集为x<1,关于x的不等式组$\left\{\begin{array}{l}{mx<0}\\{kx-b<0}\end{array}\right.$的解集为-3<x<0. 分析 直线y=kx+b落在y=mx的上方对应的x的取值范围就是关于x的不等式(k-m)x+b>0的解集;根据一次函数y=kx+b(k,b为常数,且k≠0)的图象与x轴相交于点A(3,0),得到b=-3k,k<0,再求出kx-b<0的解集,根据图象得到mx<0的解集是x<0,进而得到关于x的不等式组$\left\{\begin{array}{l}{mx<0}\\{kx-b<0}\end{array}\right.$的解集.
解答 解:∵正比例函数y=mx(m为常数,且m≠0)的图象与一次函数y=kx+b的图象相交于点P,且点P的横坐标为1,
∴关于x的不等式(k-m)x+b>0的解集为x<1;
∵一次函数y=kx+b(k,b为常数,且k≠0)的图象与x轴相交于点A(3,0),且y随x的增大而减小,
∴3k+b=0,b=-3k,k<0,
∴kx-b<0的解集是x>-3,
∵正比例函数y=mx,y随x的增大而增大,
∴mx<0的解集是x<0,
∴关于x的不等式组$\left\{\begin{array}{l}{mx<0}\\{kx-b<0}\end{array}\right.$的解集为-3<x<0.
故答案为x<1;-3<x<0.
点评 本题考查了一次函数与一元一次不等式的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.


科目:初中数学 来源: 题型:解答题
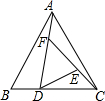 如图,在△ABC中,已知△ABC的面积为1,BD=$\frac{1}{2}$DC,AF=$\frac{1}{2}$FD,CE=$\frac{1}{2}$EF,求△DEF的面积.
如图,在△ABC中,已知△ABC的面积为1,BD=$\frac{1}{2}$DC,AF=$\frac{1}{2}$FD,CE=$\frac{1}{2}$EF,求△DEF的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
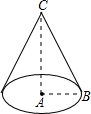 如图,在Rt△ABC中,∠BAC=90°,AB=2,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的表面积为( )
如图,在Rt△ABC中,∠BAC=90°,AB=2,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的表面积为( )| A. | 10π | B. | 12π | C. | 14π | D. | 16π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知平面直角坐标系xOy,已知二次函数y=x2-2bx+3的图象过x轴上点A(3,0),且与y轴交于点B,顶点为点P.
已知平面直角坐标系xOy,已知二次函数y=x2-2bx+3的图象过x轴上点A(3,0),且与y轴交于点B,顶点为点P.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com