
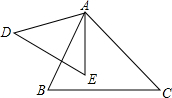
 如图所示,在△ABC与△ADE中,AB•ED=AE•BC,要使△ABC与△ADE相似,还需要添加一个条件,这个条件是∠B=∠E(答案不唯一)(只加一个即可)并证明.
如图所示,在△ABC与△ADE中,AB•ED=AE•BC,要使△ABC与△ADE相似,还需要添加一个条件,这个条件是∠B=∠E(答案不唯一)(只加一个即可)并证明. 分析 根据相似三角形的判定定理进行解答即可.
解答 解:条件①,∠B=∠E.
证明:∵AB•ED=AE•BC,
∴$\frac{AB}{AE}$=$\frac{BC}{EC}$.
∵∠B=∠E,
∴△ABC∽△AED.
条件②,$\frac{AD}{AC}$=$\frac{AE}{AB}$.
证明:∵AB•ED=AE•BC,
∴$\frac{AB}{AE}$=$\frac{BC}{EC}$.
∵$\frac{AD}{AC}$=$\frac{AE}{AB}$,
∴$\frac{AB}{AE}$=$\frac{BC}{EC}$=$\frac{AC}{AD}$,
∴△ABC∽△AED.
故答案为:∠B=∠E(答案不唯一).
点评 本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:解答题
 如图,点O是直线AB上的一点,OC是∠AOD的平分线,已知∠BOD的余角等于∠AOC的$\frac{1}{3}$,求∠BOD的邻补角的度数.
如图,点O是直线AB上的一点,OC是∠AOD的平分线,已知∠BOD的余角等于∠AOC的$\frac{1}{3}$,求∠BOD的邻补角的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
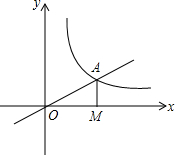 如图,正比例y=$\frac{1}{2}$x的图象与y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.如果B为及比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,P为x轴上一点,求使PA+PB的值最小时点P坐标.
如图,正比例y=$\frac{1}{2}$x的图象与y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.如果B为及比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,P为x轴上一点,求使PA+PB的值最小时点P坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
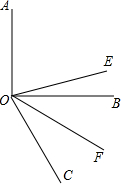 如图,已知OE平分∠AOC,OF平分∠BOC
如图,已知OE平分∠AOC,OF平分∠BOC查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 景点 | 频数 | 频率 |
| 甲 | 45 | b |
| 乙 | a | 0.3 |
| 丙 | 105 | 0.35 |
| 丁 | 60 | c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com