
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,$\sqrt{3}$) | B. | (-$\sqrt{3}$,-1) | C. | ($\sqrt{3}$,-1) | D. | ($\sqrt{3}$,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
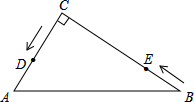 如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C→A→B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为ts(0<t<8).
如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C→A→B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为ts(0<t<8).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
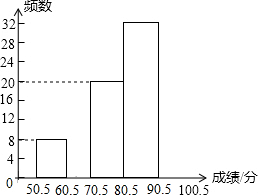 某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:
某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:| 分组 | 频数 | 频率 |
| 50.5-60.5 | 8 | 0.08 |
| 60.5-70.5 | 12 | 0.12 |
| 70.5-80.5 | 20 | 0.2 |
| 80.5-90.5 | 32 | 0.32 |
| 90.5-100.5 | 28 | a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com