
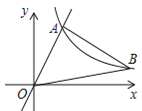
【题目】如图,在平面直角坐标系中,经过点A的双曲线![]() 同时经过点B,且点A在点B的左侧,点A的横坐标为
同时经过点B,且点A在点B的左侧,点A的横坐标为![]() ,∠AOB=∠OBA=45°,则
,∠AOB=∠OBA=45°,则![]() 的值为_________.
的值为_________.
【答案】1+![]()
【解析】分析:过A作AM⊥y轴于M,过B作BD垂直x轴于D,直线BD与AM交于点N,则OD=MN,DN=OM,∠AMO=∠BNA=90°,由等腰三角形的判定与性质得出OA=BA,∠OAB=90°,证出∠AOM=∠BAN,由AAS证明△AOM≌△BAN,得出AM=BN=![]() ,OM=AN=
,OM=AN=![]() ,求出B(
,求出B(![]() +
+![]() ,
,![]()
![]() ),得出方程(
),得出方程(![]() +
+![]() )(
)(![]()
![]() )=k,解方程即可.
)=k,解方程即可.
详解:过A作AM⊥y轴于M,过B作BD垂直x轴于D,直线BD与AM交于点N,如图所示: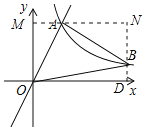
则OD=MN,DN=OM,∠AMO=∠BNA=90°,
∴∠AOM+∠OAM=90°,
∵∠AOB=∠OBA=45°,
∴OA=BA,∠OAB=90°,
∴∠OAM+∠BAN=90°,
∴∠AOM=∠BAN,
在△AOM和△BAN中,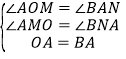 ,
,
∴△AOM≌△BAN(AAS),
∴AM=BN=![]() ,OM=AN=
,OM=AN=![]() ,
,
∴OD=![]() +
+![]() ,BD=
,BD=![]()
![]() ,
,
∴B(![]() +
+![]() ,
,![]()
![]() ),
),
∴双曲线y=![]() (x>0)同时经过点A和B,
(x>0)同时经过点A和B,
∴(![]() +
+![]() )(
)(![]()
![]() )=k,
)=k,
整理得:k2k4=0,
解得:k=1±![]() (负值舍去),
(负值舍去),
∴k=1+![]() ;
;
故答案为:1+![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】(2016广西桂林市)已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=![]() (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p=![]() ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5,∴p=![]() =6,∴S=
=6,∴S=![]() =
=![]() =6.
=6.
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
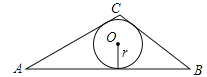
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:已知在纸面上有一数轴(如图所示).
![]()
左右折叠纸面,折痕所在的直线与数轴的交点为“对折中心点”
操作一:
(1)左右折叠纸面,使1表示的点与-1表示的点重合,则-3表示的点与 表示的点重合;
操作二:
(2)左右折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
①对折中心点所表示的数为 ,对折后5表示的点与数 表示的点重合;
②若数轴上A.B两点之间距离为11(A在B的左侧),且A.B两点经折叠后重合,求A.B两点表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD是弦,且AB![]() CD于点E。连接AC、OC、BC。
CD于点E。连接AC、OC、BC。
(1)求证: ![]() ACO=
ACO=![]() BCD。
BCD。
(2)若EB=![]() ,CD=
,CD=![]() ,求⊙O的直径。
,求⊙O的直径。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2分别是8×6的网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上,请在图1、图2中各画一个图形,分别满足以下要求:
(1)在图1中画一个以线段AB为一边周长为10+2![]() 的平行四边形,所画图形的各顶点必须在小正方形的顶点上.
的平行四边形,所画图形的各顶点必须在小正方形的顶点上.
(2)在图2中画一个以线段AB为一边的等腰三角形,所画等腰三角形的各顶点必须在小正方形的顶点上,并求出该等腰三角形的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜加工公司先后两批收购蒜苔(tái)共100吨,第一批蒜苔价格为1万元/吨;因蒜苔大量上市,第二批价格跌至0.4万元/吨,这两批蒜苔共用去52万元.
(1)求两批各购进蒜苔多少吨?
(2)公司收购后对蒜苔进行加工,分为粗加工和精加工两种.粗加工每吨利润400元,精加工每吨利润1600元要求精加工数量不大于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边的中点,分别过点B、C作射线AD的垂线,垂足分别为E、F,连接BF、CE.
(1)求证:四边形BECF是平行四边形;
(2)若AF=FD,在不添加辅助线的条件下,直接写出与△ABD面积相等的所有三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知长方形纸片![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,将
上,将![]() 沿
沿![]() 翻折到
翻折到![]() ,射线
,射线![]() 与
与![]() 交于点
交于点![]() .点
.点![]() 在边
在边![]() 上,将
上,将![]() 沿
沿![]() 翻折到
翻折到![]() ,射线
,射线![]() 与
与![]() 交于点
交于点![]() .
.
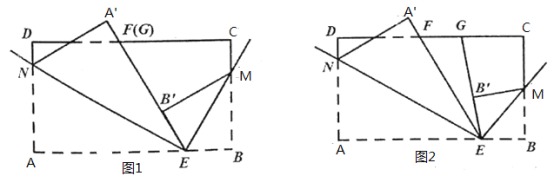
(1)如图1,若点![]() 与点
与点![]() 重合,直接写出以
重合,直接写出以![]() 为顶点的两对相等的角,并求
为顶点的两对相等的角,并求![]() 的度数;
的度数;
(2)如图2,若点![]() 在点
在点![]() 的右侧,且
的右侧,且![]() ,
,![]() ,求
,求![]() 与
与![]() 的度数;
的度数;
(3)若点![]() 在点
在点![]() 的左侧,且
的左侧,且![]() ,求
,求![]() 的度数(用含
的度数(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com