
”¾ĢāÄæ”æŅŃÖŖÅ×ĪļĻßy£½ax2+bx+c(a£¼0)µÄ¶„µćM(1£¬©4a)£¬ĒŅ¹żµćA(4£¬t)£¬ÓėxÖį½»ÓŚB”¢CĮ½µć(µćBŌŚµćCµÄ×ó²ą)£¬Ö±Ļßl¾¹żµćA£¬B£¬½»yÖį½»ÓŚµćD.
(1)Čōa£½©1£¬µ±2”Üx£¼4Ź±£¬ĒóyµÄ·¶Ī§£»
(2)Čō”÷MBCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬Ēó”÷ABMµÄĆ껿£»
(3)µćEŹĒÖ±ĻßlÉĻ·½µÄÅ×ĪļĻßÉĻµÄ¶Æµć£¬”÷BDEµÄĆ껿µÄ×ī“óÖµĪŖ![]() £»ÉčPŹĒÅ×ĪļĻߵĶŌ³ĘÖįÉĻµÄŅ»µć£¬µćQŌŚÅ×ĪļĻßÉĻ£¬ŅŌµćA”¢B”¢P”¢QĪŖ¶„µćµÄĖıߊĪÄÜ·ńĪŖ¾ŲŠĪ£æČōÄÜ£¬Ēó³öµćPµÄ×ų±ź£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ.
£»ÉčPŹĒÅ×ĪļĻߵĶŌ³ĘÖįÉĻµÄŅ»µć£¬µćQŌŚÅ×ĪļĻßÉĻ£¬ŅŌµćA”¢B”¢P”¢QĪŖ¶„µćµÄĖıߊĪÄÜ·ńĪŖ¾ŲŠĪ£æČōÄÜ£¬Ēó³öµćPµÄ×ų±ź£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ.
”¾“š°ø”æ(1) ©5£¼y”Ü3£»(2)”÷ABMµÄĆ껿£½4£»(3)ŅŌµćA”¢D”¢P”¢QĪŖ¶„µćµÄĘ½ŠŠĖıߊĪ¶¼²»æÉÄÜŹĒ¾ŲŠĪ£¬ĄķÓɼū½āĪö.
”¾½āĪö”æ
(1)a£½©1Ź±£¬y£½©(x©3)(x+1)£¬µ±x£½2Ź±£¬y£½3£¬µ±x£½4Ź±£¬y£½©5£¬¼“æÉĒó½ā£»
(2)”÷MBCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬ŌņyM£½![]() BC£½2£¬”÷ABMµÄĆ껿£½
BC£½2£¬”÷ABMµÄĆ껿£½![]() ”ĮCB”ĮyM£½
”ĮCB”ĮyM£½![]() ”Į4”Į2£½4£»
”Į4”Į2£½4£»
(3)S”÷ACE£½S”÷AFE©S”÷CFE£¬½āµĆa£½©1£»·ÖADŹĒĘ½ŠŠĖıߊĪµÄŅ»Ģõ±ß”¢ADŹĒĘ½ŠŠĖıߊĪµÄŅ»Ģõ¶Ō½ĒĻߣ¬·Ö±šĒó½ā¼“æÉ.
½ā£ŗy£½a(x©1)2©4a£½ax2©2ax©3a£¬
Įīy£½0£¬Ōņ0£½ax2©2ax©3a£¬
½āµĆx1£½©1£¬x2£½3
”ßµćAŌŚµćBµÄ×ó²ą£¬
”ąA(©1£¬0)£¬
”ßÖ±Ļßl¾¹żµćA£¬
”ą0£½©k+b£¬b£½k£¬
”ąy£½kx+k£¬
”ßµćDµÄŗį×ų±źĪŖ4£¬Įīax2©2ax©3a£½kx+k£¬
”ąa”Į42©2a”Į4©3a£½k”Į4+k£¬
”ąk£½a£¬
”ąÖ±ĻßlµÄŗÆŹż±ķ“ļŹ½ĪŖy£½ax+a£»
(1)a£½©1Ź±£¬y£½©(x©3)(x+1)£¬
µ±x£½2Ź±£¬y£½3£¬µ±x£½4Ź±£¬y£½©5£¬
¹Ź©5£¼y”Ü3£»
(2)”÷MBCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬ŌņyM£½![]() BC£½2£¬
BC£½2£¬
”÷ABMµÄĆ껿£½![]() ”ĮCB”ĮyM£½
”ĮCB”ĮyM£½![]() 4”Į2£½4£»
4”Į2£½4£»
(3)Čē“šĶ¼1£¬¹żµćE×÷EF”ĪyÖį£¬½»Ö±ĻßlÓŚµćF£¬
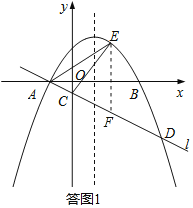
ÉčE(x£¬ax2©2ax©3a)£¬ŌņF(x£¬ax+a)
EF£½ax2©2ax©3a©(ax+a)£½ax2©3ax©4a
S”÷ACE£½S”÷AFE©S”÷CFE
£½![]() (ax2©3ax©4a)(x+1)©
(ax2©3ax©4a)(x+1)©![]() (ax2©3ax©4a)x
(ax2©3ax©4a)x
£½![]() (ax2©3ax©4a)£½
(ax2©3ax©4a)£½![]() a(x©
a(x©![]() )2©
)2©![]() a£¬
a£¬
”ą”÷ACEµÄĆ껿µÄ×ī“óÖµĪŖ©![]() a£¬
a£¬
”ß”÷ACEµÄĆ껿µÄ×ī“óÖµĪŖ![]() £¬
£¬
”ą©![]() a£½
a£½![]() £¬
£¬
½āµĆa£½©1£»
Å×ĪļĻß½āĪöŹ½ĪŖy£½©x2+2x+3£¬
”ąA(©1£¬0)£¬D(4£¬©5)£¬
”ąA”¢DµćµÄŗį×ų±źĻą²ī5£¬
”ąÅ×ĪļĻߵĶŌ³ĘÖįĪŖx£½1£¬
”ąPµćµÄŗį×ų±źŹĒ1£¬
¢ŁČē“šĶ¼2£¬ČōADŹĒĘ½ŠŠĖıߊĪµÄŅ»Ģõ±ß£¬AD”ĪQP£¬ŌņµćPÓėµćQµÄŗį×ų±źĻą²ī5£¬ŌņQµćŗį×ų±źŹĒ©4£¬

”ąQ(©4£¬©21)£»
¢ŚČē“šĶ¼3£¬ČōADŹĒĘ½ŠŠĖıߊĪµÄŅ»Ģõ¶Ō½ĒĻߣ¬
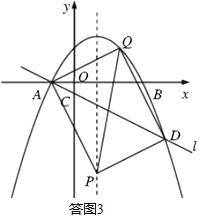
ŌņĻ߶ĪADµÄÖŠµćµÄŗį×ų±źŹĒ![]() £¬
£¬
”ßPµćµÄŗį×ų±źŹĒ1£¬
”ąQµćŗį×ų±źŹĒ2£¬
”ąQ(2£¬3)£¬
¾ŃéÖ¤ŅŌÉĻĮ½ÖÖŅŌµćA”¢D”¢P”¢QĪŖ¶„µćµÄĘ½ŠŠĖıߊĪ¶¼²»æÉÄÜŹĒ¾ŲŠĪ.


 ¾«Ó¢æŚĖćæØĻµĮŠ“š°ø
¾«Ó¢æŚĖćæØĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”放ĢāÄæ”æČēĶ¼¢Ł£¬Ņ»“ĪŗÆŹż y£½![]() x - 2 µÄĶ¼Ļń½» x ÖįÓŚµć A£¬½» y ÖįÓŚµć B£¬¶ž“ĪŗÆŹż y£½
x - 2 µÄĶ¼Ļń½» x ÖįÓŚµć A£¬½» y ÖįÓŚµć B£¬¶ž“ĪŗÆŹż y£½![]() x2 bx cµÄĶ¼Ļń¾¹ż A”¢B Į½µć£¬Óė x Öį½»ÓŚĮķŅ»µć C£®
x2 bx cµÄĶ¼Ļń¾¹ż A”¢B Į½µć£¬Óė x Öį½»ÓŚĮķŅ»µć C£®
£Ø1£©Ē󶞓ĪŗÆŹżµÄ¹ŲĻµŹ½¼°µć C µÄ×ų±ź£»
£Ø2£©ČēĶ¼¢Ś£¬Čōµć P ŹĒÖ±Ļß AB ÉĻ·½µÄÅ×ĪļĻßÉĻŅ»µć£¬¹żµć P ×÷ PD”Īx Öį½» AB ÓŚµć D£¬PE”Īy Öį½» AB ÓŚµć E£¬Ēó PD£«PE µÄ×ī“óÖµ£»
£Ø3£©ČēĶ¼¢Ū£¬Čōµć M ŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻ£¬ĒŅ”ĻAMB£½”ĻACB£¬Ēó³öĖłÓŠĀś×ćĢõ¼žµÄµć MµÄ×ų±ź£®
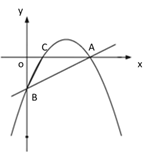
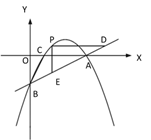
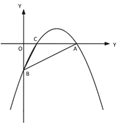
¢Ł ¢Ś ¢Ū
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŅŹŠÄ³ĻēÕņŌŚ”°¾«×¼·öʶ”±»ī¶ÆÖŠĻśŹŪÅ©²śĘ·£¬¾·ÖĪö·¢ĻÖŌĀĻśŹŪĮæ![]() (Ķņ¼žÓėŌĀ·Ż
(Ķņ¼žÓėŌĀ·Ż![]() (ŌĀ)µÄ¹ŲĻµĪŖ:
(ŌĀ)µÄ¹ŲĻµĪŖ: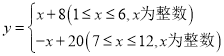
Ć漞²śĘ·µÄĄūČó![]() (ŌŖ)ÓėŌĀ·Ż
(ŌŖ)ÓėŌĀ·Ż![]() (ŌĀ)µÄ¹ŲĻµČēĻĀ±ķ:
(ŌĀ)µÄ¹ŲĻµČēĻĀ±ķ:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
![]() ĒėÄćøł¾Ż±ķøńÖ±½ÓŠ“³öĆ漞²śĘ·ĄūČóz (ŌŖ) ÓėŌĀ·Ż
ĒėÄćøł¾Ż±ķøńÖ±½ÓŠ“³öĆ漞²śĘ·ĄūČóz (ŌŖ) ÓėŌĀ·Ż![]() (ŌĀ)µÄŗÆŹż¹ŲĻµŹ½;
(ŌĀ)µÄŗÆŹż¹ŲĻµŹ½;
![]() ČōŌĀĄūČó
ČōŌĀĄūČó![]() (ĶņŌŖ) =µ±ŌĀĻśŹŪĮæ
(ĶņŌŖ) =µ±ŌĀĻśŹŪĮæ![]() (Ķņ¼ž)
(Ķņ¼ž) ![]() µ±ŌĀĆ漞²śĘ·µÄĄūČó
µ±ŌĀĆ漞²śĘ·µÄĄūČó![]() (ŌŖ)£¬ĒóŌĀĄūČó
(ŌŖ)£¬ĒóŌĀĄūČó![]() (ĶņŌŖ)ÓėŌĀ·Ż
(ĶņŌŖ)ÓėŌĀ·Ż![]() (ŌĀ)µÄ¹ŲĻµŹ½;
(ŌĀ)µÄ¹ŲĻµŹ½;
![]() µ±
µ±![]() ĪŖŗĪÖµŹ±£¬ŌĀĄūČó
ĪŖŗĪÖµŹ±£¬ŌĀĄūČó![]() ÓŠ×ī“óÖµ£¬×ī“óÖµĪŖ¶ąÉŁ?
ÓŠ×ī“óÖµ£¬×ī“óÖµĪŖ¶ąÉŁ?
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ½āijŹŠŹŠĆń”°ĀĢÉ«³öŠŠ”±·½Ź½µÄĒéæö£¬Ä³Š£ŹżŃ§ŠĖȤŠ”×éŅŌĪŹ¾ķµ÷²éµÄŠĪŹ½£¬Ė껜µ÷²éĮĖijŹŠ²æ·Ö³öŠŠŹŠĆńµÄÖ÷ŅŖ³öŠŠ·½Ź½£Ø²ĪÓėĪŹ¾ķµ÷²éµÄŹŠĆń¶¼Ö»“ÓŅŌĻĀĪåøöÖÖĄąÖŠŃ”ŌńŅ»Ąą£©£¬²¢½«µ÷²é½į¹ū»ęÖĘ³ÉČēĻĀ²»ĶźÕūµÄĶ³¼ĘĶ¼£®
ÖÖĄą | A | B | C | D | E |
³öŠŠ·½Ź½ | ¹²Ļķµ„³µ | ²½ŠŠ | ¹«½»³µ | µÄŹæ | Ė½¼Ņ³µ |
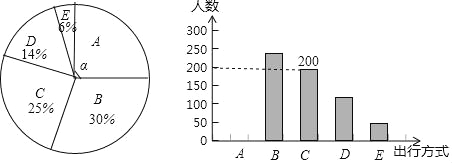
øł¾ŻŅŌÉĻŠÅĻ¢£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©²ĪÓė±¾“ĪĪŹ¾ķµ÷²éµÄŹŠĆń¹²ÓŠ ČĖ£¬ĘäÖŠŃ”ŌńBĄąµÄČĖŹżÓŠ ČĖ£»
£Ø2£©ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬ĒóAĄą¶ŌÓ¦ÉČŠĪŌ²ŠÄ½Ē¦ĮµÄ¶ČŹż£¬²¢²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
£Ø3£©øĆŹŠŌ¼ÓŠ12ĶņČĖ³öŠŠ£¬Čō½«A£¬B£¬CÕāČżĄą³öŠŠ·½Ź½¾łŹÓĪŖ”°ĀĢÉ«³öŠŠ”±·½Ź½£¬Ēė¹Ą¼ĘøĆŹŠ”°ĀĢÉ«³öŠŠ”±·½Ź½µÄČĖŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
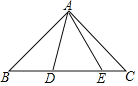
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻBAC£½90”ć£¬AB£½AC£¬µćD£¬E¾łŌŚ±ßBCÉĻ£¬ĒŅ”ĻDAE£½45”ć
(1)ČōBD£½2£¬CE£½4£¬ŌņDE£½_____.
(2)Čō”ĻAEB£½75”ć£¬ŌņĻ߶ĪBDÓėCEµÄŹżĮæ¹ŲĻµŹĒ______.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
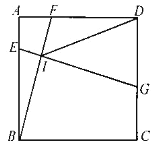
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ±ß³¤ĪŖ6µÄÕż·½ŠĪABCDÖŠ£¬µćE”¢F”¢G·Ö±šŌŚ±ßAB”¢AD”¢CDÉĻ£¬EGÓėBF½»ÓŚµćI£¬AE=2£¬BF=EG£¬DG>AE£¬ŌņDIµÄ×īŠ”ÖµĪŖ________.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ2019Äź2ŌĀ£¬ĆĄ¹śÓīŗ½¾Ö£ØNASA£©µÄĪĄŠĒ¼ą²āŹż¾ŻĻŌŹ¾µŲĒņÕżŌŚ±äĀĢ£¬·ÖĪö·¢ĻÖŹĒÖŠ¹śŗĶÓ”¶ČµÄŠŠ¶ÆÖ÷µ¼ĮĖµŲĒņ±äĀĢ£®¾”¹ÜÖŠ¹śŗĶÓ”¶ČµÄĶĮµŲĆ껿¼ÓĘšĄ“Ö»Õ¼Č«ĒņµÄ9%£¬µ«¹żČ„20Äź¼äµŲĒņČż·ÖÖ®Ņ»µÄŠĀŌöÖ²±»ŹĒĮ½¹ś¹±Ļ׵ģ¬Ć껿Ļąµ±ÓŚŅ»øöŃĒĀķŃ·ÓźĮÖ£®ŅŃÖŖŃĒĀķŃ·ÓźĮÖµÄĆ껿ĪŖ6560000km![]() £¬Ōņ¹żČ„20Äź¼äµŲĒņŠĀŌöÖ²±»µÄĆ껿Ō¼ĪŖ£Ø £©
£¬Ōņ¹żČ„20Äź¼äµŲĒņŠĀŌöÖ²±»µÄĆ껿Ō¼ĪŖ£Ø £©
A.6.56”Į10![]() km
km![]() B.6.56”Į10
B.6.56”Į10![]() km
km![]() C.2”Į10
C.2”Į10![]() km
km![]() D.2”Į10
D.2”Į10![]() km
km![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖA(©4£¬a)£¬B(©1£¬2)ŹĒŅ»“ĪŗÆŹży1=kx+bÓė·“±ČĄżŗÆŹży2=![]() (m£¼0)Ķ¼ĻóµÄĮ½øö½»µć£¬AC”ĶxÖįÓŚC£®
(m£¼0)Ķ¼ĻóµÄĮ½øö½»µć£¬AC”ĶxÖįÓŚC£®

(1)Ēó³ök£¬b¼°mµÄÖµ£®
(2)øł¾ŻĶ¼ĻóÖ±½Ó»Ų“š£ŗŌŚµŚ¶žĻóĻŽÄŚ£¬µ±y1£¾y2Ź±£¬xµÄȔֵ·¶Ī§ŹĒ ________£®
(3)ČōPŹĒĻ߶ĪABÉĻµÄŅ»µć£¬Į¬½ÓPC£¬Čō”÷PCAµÄĆ껿µČÓŚ![]() £¬ĒóµćP×ų±ź£®
£¬ĒóµćP×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖĪ¬»¤ĆæøöŃ§ÉśĘ½µČ½ÓŹÜ½ĢÓżµÄČØĄū£¬ĪŅĒųŠ”ѧ¶ąÄźĄ“×ńÕÕ”°¾Ķ½ü»®Ę¬Čėѧ”±ŌŌņŹµŠŠŃō¹āÕŠÉś£¬µēÄŌĖ껜·Ö°ą£¬·Ö°ąŹ±¶ŌĖłÓŠŃ§ÉśŅ»ŹÓĶ¬ČŹ£®Š”ŗģŗĶŠ”Ą¼Į½øöÅ®ŗ¢ŹĒĮŚ¾Ó£¬½ńÄźĻÄĢģ±»»®·Öµ½³ĒĒųµÄĶ¬Ņ»ĖłŠ”ѧ£¬ÕāĖłŃ§Š£Ņ»Äź¼¶ÓŠ1°ą”¢2°ą”¢3°ą”¢4°ą¹²ĖÄøö°ą£®ĻĀĆęŹĒ·Ö°ąĒ°Į½øöÅ®ŗ¢¼Ņ³¤µÄŅ»¶Ī¶Ō»°£ŗ
Š”ŗģĀčĀčĖµ£ŗ”°ÕęĻ£ĶūĖżĮ©ÄÜ·Öµ½Ķ¬Ņ»øö°ą£®”±
Š”Ą¼ĀčĀčĖµ£ŗ”°ĖżĮ©æÉÄÜ·Öµ½Ķ¬Ņ»øö°ą£¬Ņ²æÉÄÜ·Ö²»µ½Ķ¬Ņ»øö°ą£¬ĖłŅŌĖżĮ©·Öµ½Ķ¬Ņ»øö°ąµÄæÉÄÜŠŌŹĒ50%£®”±
ĒėÄćÓĆĖłŃ§µÄÖŖŹ¶·ÖĪöŠ”Ą¼ĀčĀčµÄĖµ·ØŹĒ·ńÕżČ·£¬ČēÕżČ·£¬ĒėĖµĆ÷ĄķÓÉ£»Čē²»ÕżČ·ĒėÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·ØĒó³öŠ”ŗģŗĶŠ”Ą¼·Öµ½Ķ¬Ņ»øö°ąµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com