
分析 (1)分别根据有理数乘方的法则、负整数指数幂的运算法则、特殊角的三角函数值及绝对值的性质计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先算括号里面的,再算除法,最后把x=-2代入进行计算即可.
解答 解:(1)原式=-4-3+2×$\frac{\sqrt{3}}{2}$-($\sqrt{3}$-1)
=-4-3+$\sqrt{3}$-$\sqrt{3}$+1
=-7+1
=-6.
(2)原式=[$\frac{x+1}{x-1}$-(x+1)]•$\frac{x-1}{x+1}$
=$\frac{x+1}{x-1}$•$\frac{x-1}{x+1}$-(x+1)•$\frac{x-1}{x+1}$
=1-(x-1)
=1-x+1
=2-x.
当x=-2时,原式=2+2=4.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.


科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.4m,∠DCF=30°,请你计算车位所占的宽度EF约为多少米.(结果精确到0.1m,$\sqrt{3}$≈1.73)
如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.4m,∠DCF=30°,请你计算车位所占的宽度EF约为多少米.(结果精确到0.1m,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
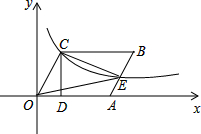 已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数$y=\frac{8}{x}$的图象经过点C,且与AB交于点E,若OD=2,则△OCE的面积为4$\sqrt{5}$.
已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数$y=\frac{8}{x}$的图象经过点C,且与AB交于点E,若OD=2,则△OCE的面积为4$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$是有理数 | B. | 面积为12的正方形边长是$\sqrt{12}$ | ||
| C. | $\sqrt{12}$=2$\sqrt{3}$ | D. | 在数轴上可以找到表示$\sqrt{12}$的点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
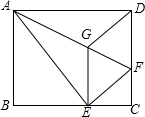 如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.
如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com