
【题目】如图,抛物线![]() (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
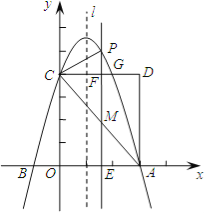
(1)求抛物线的解析式;
(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;
(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由。
【答案】解:(1)∵抛物线![]() (a≠0)经过点A(3,0),点C(0,4),
(a≠0)经过点A(3,0),点C(0,4),
∴![]() ,解得
,解得 。
。
∴抛物线的解析式为![]() 。
。
(2)设直线AC的解析式为y=kx+b,
∵A(3,0),点C(0,4),
∴![]() ,解得
,解得 。
。
∴直线AC的解析式为![]() 。
。
∵点M的横坐标为m,点M在AC上,
∴M点的坐标为(m,![]() )。
)。
研三理-孟奕含(713000529);∵点P的横坐标为m,点P在抛物线![]() 上,
上,
∴点P的坐标为(m,![]() )。
)。
∴PM=PE-ME=(![]() )-(
)-(![]() )=
)=![]() 。
。
∴PM=![]() (0<m<3)。
(0<m<3)。
(3)在(2)的条件下,连接PC,在CD上方的抛物线部分存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似。理由如下:
由题意,可得AE=3﹣m,EM=![]() ,CF=m,PF=
,CF=m,PF=![]() =
=![]() ,
,
若以P、C、F为顶点的三角形和△AEM相似,分两种情况:
①若△PFC∽△AEM,则PF:AE=FC:EM,即(![]() ):(3-m)=m:(
):(3-m)=m:(![]() ),
),
∵m≠0且m≠3,∴m=![]() 。
。
∵△PFC∽△AEM,∴∠PCF=∠AME。
∵∠AME=∠CMF,∴∠PCF=∠CMF。
在直角△CMF中,∵∠CMF+∠MCF=90°,∴∠PCF+∠MCF=90°,即∠PCM=90°。
∴△PCM为直角三角形。
②若△CFP∽△AEM,则CF:AE=PF:EM,即m:(3-m)=(![]() ):(
):(![]() ),
),
∵m≠0且m≠3,∴m=1。
∵△CFP∽△AEM,∴∠CPF=∠AME。
∵∠AME=∠CMF,∴∠CPF=∠CMF。∴CP=CM。
∴△PCM为等腰三角形。
综上所述,存在这样的点P使△PFC与△AEM相似.此时m的值为![]() 或1,△PCM为直角三角形或等腰三角形。
或1,△PCM为直角三角形或等腰三角形。
【解析】(1)将A(3,0),C(0,4)代入![]() ,运用待定系数法即可求出抛物线的解析式。
,运用待定系数法即可求出抛物线的解析式。
(2)先根据A、C的坐标,用待定系数法求出直线AC的解析式,从而根据抛物线和直线AC的解析式分别表示出点P、点M的坐标,即可得到PM的长。
(3)由于∠PFC和∠AEM都是直角,F和E对应,则若以P、C、F为顶点的三角形和△AEM相似时,分两种情况进行讨论:①△PFC∽△AEM,②△CFP∽△AEM;可分别用含m的代数式表示出AE、EM、CF、PF的长,根据相似三角形对应边的比相等列出比例式,求出m的值,再根据相似三角形的性质,直角三角形、等腰三角形的判定判断出△PCM的形状。


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】某校开展拓展课程展示活动,需要制作A,B两种型号的宣传广告共20个,已知A,B两种广告牌的单价分别为40元,70元
(1)若根据活动需要,A种广告牌数量与B种广告牌数量之比为3:2,需要多少费用?
(2)若需制作A,B两种型号的宣传广告牌,其中B种型号不少于5个,制作总费用不超过1000元,则有几种制作方案?每一种制作方案的费用分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题提出)|a﹣1|+|a﹣2|+|a﹣3|+…+|a﹣2019|最小值是多少?
(阅读理解)
为了解决这个问题,我们先从最简单的情况入手.|a|的几何意义是a这个数在数轴上对应的点到原点的距离.那么|a﹣1|可以看做a这个数在数轴上对应的点到1的距离;|a﹣1|+|a﹣2|就可以看作a这个数在数轴上对应的点到1和2两个点的距离之和.下面我们结合数轴研究|a﹣1|+|a﹣2|的最小值.
我们先看a表示的点可能的3种情况,如图所示:
(1)如图①,a在1的左边,从图中很明显可以看出a到1和2的距离之和大于1.
(2)如图②,a在1和2之间(包括在1,2上),可以看出a到1和2的距离之和等于1.
(3)如图③,a在2的右边,从图中很明显可以看出a到1和2的距离之和大于1.
(问题解决)
(1)|a﹣2|+|a﹣5|的几何意义是 .请你结合数轴探究:|a﹣2|+|a﹣5|的最小值是 .
(2)|a﹣1|+|a﹣2|+|a﹣3|的几何意义是 .请你结合数轴探究:|a﹣1|+|a﹣2|+|a﹣3|的最小值是 ,并在图④的数轴上描出得到最小值时a所在的位置,由此可以得出a为 .
(3)求出|a﹣1|+|a﹣2|+|a﹣3|+|a﹣4|+|a﹣5|的最小值.
(4)求出|a﹣1|+|a﹣2|+|a﹣3|+…+|a﹣2019|的最小值.
(拓展应用)
请在图⑤的数轴上表示出a,使它到2,5的距离之和小于4,并直接写出a的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,半圆O的直径AB=4,![]() =
=![]() ,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
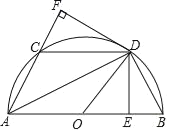
(1)求证:△CDF≌△BDE;
(2)当AD= 时,四边形AODC是菱形;
(3)当AD= 时,四边形AEDF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一只不透明的盒子里有背面完全相同,正面上分别写有数字1、2、3、4的四张卡片,小马从中随机地抽取一张,把卡片上的数字作为被减数;在另一只不透明的盒子里将形状、大小完全相同,分别标有数字1、2、3的三个小球混合后,小虎从中随机地抽取一个,把小球上的数字做为减数,然后计算出这两个数的差.
(1)请你用画树状图或列表的方法,求这两数差为0的概率;
(2)小马与小虎做游戏,规则是:若这两数的差为非正数,则小马赢;否则小虎赢.你认为该游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“过圆上一点作圆的切线”的尺规作图过程.
已知:⊙O和⊙O上一点P.
求作:⊙O的切线MN,使MN经过点P.

作法:如图,
(1)作射线OP;
(2)以点P为圆心,小于OP的长为半径作弧交射线OP于A,B两点;
(3)分别以点A,B为圆心,以大于![]() 长为半径作弧,两弧交于M,N两点;
长为半径作弧,两弧交于M,N两点;
(4)作直线MN.则MN就是所求作的⊙O的切线.
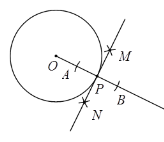
请回答:该尺规作图的依据是____________________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 和矩形
和矩形![]() 的边
的边![]() 都在直线
都在直线![]() 上,以点
上,以点![]() 为圆心,以24为半径作半圆,分别交直线
为圆心,以24为半径作半圆,分别交直线![]() 于
于![]() 两点.已知:
两点.已知: ![]() ,
,![]() ,矩形自右向左在直线
,矩形自右向左在直线![]() 上平移,当点
上平移,当点![]() 到达点
到达点![]() 时,矩形停止运动.在平移过程中,设矩形对角线
时,矩形停止运动.在平移过程中,设矩形对角线![]() 与半圆
与半圆![]() 的交点为
的交点为![]() (点
(点![]() 为半圆上远离点
为半圆上远离点![]() 的交点).
的交点).
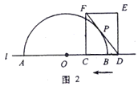
(1)如图2,若![]() 与半圆
与半圆![]() 相切,求
相切,求![]() 的值;
的值;
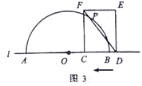
(2)如图3,当![]() 与半圆
与半圆![]() 有两个交点时,求线段
有两个交点时,求线段![]() 的取值范围;
的取值范围;
(3)若线段![]() 的长为20,直接写出此时
的长为20,直接写出此时![]() 的值.
的值.
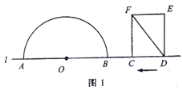
查看答案和解析>>
科目:初中数学 来源: 题型:
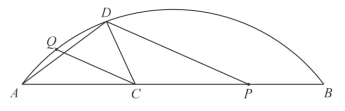
【题目】如图,Q是![]() 上一定点,P是弦AB上一动点,C为AP中点,连接CQ,过点P作
上一定点,P是弦AB上一动点,C为AP中点,连接CQ,过点P作![]() 交
交![]() 于点D,连接AD,CD.
于点D,连接AD,CD.
已知![]() ,设A,P两点间的距离为
,设A,P两点间的距离为![]() ,C,D两点间的距离为
,C,D两点间的距离为![]() .
.
(当点P与点A重合时,令y的值为1.30)
小荣根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探宄.
下面是小荣的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值:

(2)建立平面直角坐标系,描出以补全后的表中各组对应值为坐标的点,画出该函数的图象;

(3)结合函数图象,解决问题:当![]() 时,AP的长度约为__________cm.
时,AP的长度约为__________cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com