
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3). 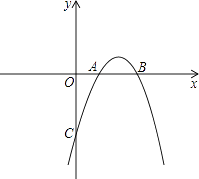
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式.
【答案】
(1)解:∵抛物线与x轴交于点A(1,0),B(3,0),
可设抛物线解析式为y=a(x﹣1)(x﹣3),
把C(0,﹣3)代入得:3a=﹣3,
解得:a=﹣1,
故抛物线解析式为y=﹣(x﹣1)(x﹣3),
即y=﹣x2+4x﹣3,
∵y=﹣x2+4x﹣3=﹣(x﹣2)2+1,
∴顶点坐标(2,1)
(2)解:先向左平移2个单位,再向下平移1个单位,得到的抛物线的解析式为y=﹣x2,平移后抛物线的顶点为(0,0)落在直线y=﹣x上(答案不唯一)
【解析】(1)利用交点式得出y=a(x﹣1)(x﹣3),进而得出a的值,再利用配方法求出顶点坐标即可;(2)根据左加右减得出抛物线的解析式为y=﹣x2 , 进而得出答案.
【考点精析】通过灵活运用二次函数图象的平移,掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+4与x轴、y轴分别交于点A、B,点C从点B出发,以每秒5个单位长度的速度向点A匀速运动;同时点D从点O出发,以每秒4个单位长度的速度向点B匀速运动,到达终点后运动立即停止.连接CD,取CD的中点E,过点E作EF⊥CD,与折线DO﹣OA﹣AC交于点F,设运动时间为t秒.
x+4与x轴、y轴分别交于点A、B,点C从点B出发,以每秒5个单位长度的速度向点A匀速运动;同时点D从点O出发,以每秒4个单位长度的速度向点B匀速运动,到达终点后运动立即停止.连接CD,取CD的中点E,过点E作EF⊥CD,与折线DO﹣OA﹣AC交于点F,设运动时间为t秒.
(1)点C的坐标为(用含t的代数式表示);
(2)求证:点E到x轴的距离为定值;
(3)连接DF、CF,当△CDF是以CD为斜边的等腰直角三角形时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC,在△ABC外侧作直线CP,点A关于直线CP的对称点为D,连接AD,BD,其中BD交直线CP于点E.
(1)如图1,∠ACP=15°.
①依题意补全图形;
②求∠CBD的度数;
(2)如图2,若45°<∠ACP<90°,直接用等式表示线段AC,DE,BE之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(﹣4,0),点P在射线AB上运动,连结CP与y轴交于点D,连结BD.过P,D,B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF,BF.
(1)求直线AB的函数解析式;
(2)当点P在线段AB(不包括A,B两点)上时.
①求证:∠BDE=∠ADP;
②设DE=x,DF=y.请求出y关于x的函数解析式;
(3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标:如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一节地理课结束后,小明拿出地球仪,突发奇想:地球仪环形支架的长度比地球仪上画的赤道的长度长多少? 活动一:如图1,求大圆与小圆的周长之差?
活动二:如图2,以O为圆心,任意画出两个圆,两圆半径相差6cm,求大圆与小圆的周长之差?
活动三:若地球仪与环形支架之间的间隙为k(cm),请直接写出地球仪环形支架的长度比地球仪上画的赤道的长度长多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE. 
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com