
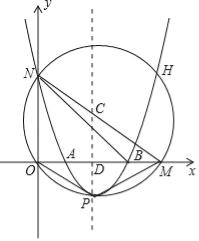
【题目】如图所示,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y轴分别相交于M(4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.
(1)求线段CD的长及顶点P的坐标;
(2)求抛物线的函数表达式;
(3)设抛物线交x轴于A,B两点,在抛物线上是否存在点Q,使得S四边形OPMN=8S△QAB,且△QAB∽△OBN成立?若存在,请求出Q点的坐标;若不存在,请说明理由.
【答案】(1) CD=![]() , P(2,﹣1);(2) y=x2﹣4x+3;(3) 存在满足条件的点Q,其坐标为(2,﹣1).
, P(2,﹣1);(2) y=x2﹣4x+3;(3) 存在满足条件的点Q,其坐标为(2,﹣1).
【解析】试题分析:(1)连接OC,由勾股定理可求得MN的长,则可求得OC的长,由垂径定理可求得OD的长,在Rt△OCD中,可求得CD的长,则可求得PD的长,可求得P点坐标;(2)可设抛物线的解析式为顶点式,再把N点坐标代入可求得抛物线解析式;(3)由抛物线解析式可求得A、B的坐标,由S四边形OPMN=8S△QAB可求得点Q到x轴的距离,且点Q只能在x轴的下方,则可求得Q点的坐标,再证明△QAB∽△OBN即可.
试题解析:
(1)如图,连接OC,

∵M(4,0),N(0,3),
∴OM=4,ON=3,
∴MN=5,
∴OC=![]() MN=
MN=![]() ,
,
∵CD为抛物线对称轴,
∴OD=MD=2,
在Rt△OCD中,由勾股定理可得CD=![]() =
=![]() ,
,
∴PD=PC﹣CD=![]() ﹣
﹣![]() =1,
=1,
∴P(2,﹣1);
(2)∵抛物线的顶点为P(2,﹣1),
∴设抛物线的函数表达式为y=a(x﹣2)2﹣1,
∵抛物线过N(0,3),
∴3=a(0﹣2)2﹣1,解得a=1,
∴抛物线的函数表达式为y=(x﹣2)2﹣1,即y=x2﹣4x+3;
(3)在y=x2﹣4x+3中,令y=0可得0=x2﹣4x+3,解得x=1或x=3,
∴A(1,0),B(3,0),
∴AB=3﹣1=2,
∵ON=3,OM=4,PD=1,
∴S四边形OPMN=S△OMP+S△OMN=![]() OMPD+
OMPD+![]() OMON=
OMON=![]() ×4×1+
×4×1+![]() ×4×3=8=8S△QAB,
×4×3=8=8S△QAB,
∴S△QAB=1,
设Q点纵坐标为y,则![]() ×2×|y|=1,解得y=1或y=﹣1,
×2×|y|=1,解得y=1或y=﹣1,
当y=1时,则△QAB为钝角三角形,而△OBN为直角三角形,不合题意,舍去,
当y=﹣1时,可知P点即为所求的Q点,
∵D为AB的中点,
∴AD=BD=QD,
∴△QAB为等腰直角三角形,
∵ON=OB=3,
∴△OBN为等腰直角三角形,
∴△QAB∽△OBN,
综上可知存在满足条件的点Q,其坐标为(2,﹣1).


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:

![]()
(1)该班总人数是 ;
(2)根据计算,请你补全两个统计图;
(3)观察补全后的统计图,写出一条你发现的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a+b<0,b>0,则下列结论:①a>b>0;②|a|<|b|;③ab<0;④b﹣a>b+a,正确的是( )
A. ①②B. ②③C. ③④D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F. 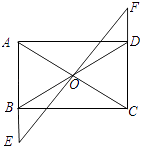
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么关系时,以A,E,C,F为顶点的四边形是菱形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列二次函数的图象,不能通过函数y=3x2的图象平移得到的是( )
A.y=3x2+2
B.y=3(x﹣1)2
C.y=3(x﹣1)2+2
D.y=2x2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com