
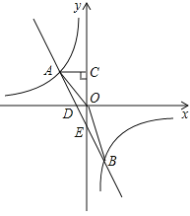
【题目】如图,在平面直角坐标系中,反比例函数![]() 与一次函数
与一次函数![]() 的图象交于
的图象交于![]() 两点,点
两点,点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() ,
, ![]() 的面积是3,一次函数
的面积是3,一次函数![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() .
.
(1)求反比例函数与一次函数的表达式;
(2)求![]() 的面积.
的面积.
【答案】(1)y=![]() ,y=-2x-1;(2)
,y=-2x-1;(2)![]()
【解析】
(1)根据![]() AOC的面积是3得到k=﹣6,于是得到反比例函数的解析式为y=
AOC的面积是3得到k=﹣6,于是得到反比例函数的解析式为y=![]() ,把B(m,﹣4)代入y=
,把B(m,﹣4)代入y=![]() 得到B(
得到B(![]() ,﹣4),设A(﹣m,n),根据已知条件得到A(﹣2,3),把A(﹣2,3),B(
,﹣4),设A(﹣m,n),根据已知条件得到A(﹣2,3),把A(﹣2,3),B(![]() ,﹣4)代入y=ax+b得到一次函数的解析式为:y=﹣2x﹣1;
,﹣4)代入y=ax+b得到一次函数的解析式为:y=﹣2x﹣1;
(2)根据三角形的面积公式即可得到结论.
解:(1)∵![]() AOC的面积是3,
AOC的面积是3,
∴k=-6,
∴反比例函数的表达式为y=![]() .
.
∵B(m,-4)在反比例函数y=![]() 的图象上,
的图象上,
∴-4m=-6,
∴m=![]() ,
,
∴B(![]() ,-4).
,-4).
设A(-m,n)(m>0,n>0),
∵tan∠AOC=![]() ,
,![]() AOC的面积是3,
AOC的面积是3,
∴![]() =
=![]() ,mn=6,
,mn=6,
∴m=2,n=3,
∴A(-2,3).
把A(-2,3),B(![]() ,-4)代入y=ax+b,
,-4)代入y=ax+b,
得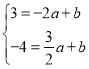
解得![]()
∴一次函数的表达式为y=-2x-1.
(2)令x=0,则y=-1,
∴E(0,-1),
∴OE=1,
∴S△AOB=S△AOE+S△BOE
=![]() ×1×2+
×1×2+![]() ×1×
×1×![]()
=![]() .
.


科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.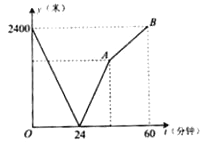
(1)根据图象信息,当t=________分钟时甲乙两人相遇,甲的速度为________米/分钟;
(2)求出线段AB所表示的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,抛物线
,抛物线![]() 与
与![]() 轴从左到右的交点为
轴从左到右的交点为![]() ,
,![]() .
.
(1)若抛物线![]() 经过点
经过点![]() ,求抛物线
,求抛物线![]() 的解析式和顶点坐标;
的解析式和顶点坐标;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
①求点![]() 的坐标;
的坐标;
②若线段![]() 与抛物线
与抛物线![]() 有唯一公共点,直接写出正整数
有唯一公共点,直接写出正整数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(2)求抛物线与![]() 轴的交点坐标;
轴的交点坐标;
(3)已知点![]() ,
,![]() ,如果抛物线与线段
,如果抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查某小区居民的用水情况,随机抽查了若干个家庭的![]() 月份用水量,结果如下表:
月份用水量,结果如下表:
月用水量(立方米) |
|
|
|
|
户数 |
|
|
|
|
根据上表解决下列问题:
(1)这组数据的众数是 ,中位数是 ;
(2)求这若干个家庭的![]() 月份平均用水量;
月份平均用水量;
(3)请根据(2)的结论估计该小区![]() 个家庭
个家庭![]() 月份总用水量.
月份总用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数关系如图2所示.
(分)的函数关系如图2所示.
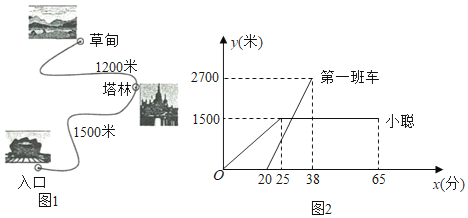
(1)求第一班车离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数表达式.
(分)的函数表达式.
(2)求第一班车从人口处到达塔林所蓄的时间.
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聘聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一种商品,其成本为每件![]() 元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于
元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于![]() .据市场调查发现,月销售量
.据市场调查发现,月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的函数关系如表:
(元)之间的函数关系如表:
销售单价 | 65 | 70 | 75 | 80 | ··· |
月销售量 | 475 | 450 | 425 | 400 | ··· |
![]() 请根据表格中所给数据,求出
请根据表格中所给数据,求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 设该网店每月获得的利润为
设该网店每月获得的利润为![]() 元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
![]() 该网店店主热心公益事业,决定每月从利润中捐出
该网店店主热心公益事业,决定每月从利润中捐出![]() 元资助贫困学生.为了保证捐款后每月利润不低于
元资助贫困学生.为了保证捐款后每月利润不低于![]() 元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
查看答案和解析>>
科目:初中数学 来源: 题型:
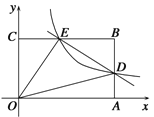
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(6,4).双曲线![]() 经过AB的中点D,且与BC交于点E,连接DE.
经过AB的中点D,且与BC交于点E,连接DE.
(1)求k的值和直线DE的解析式;
(2)若点P是y轴上一点,且△OPE的面积与四边形ODBE的面积相等,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com