
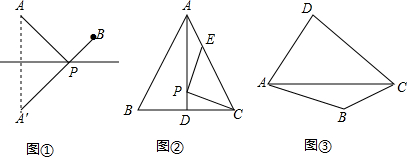
分析 (1)作点E关于AD的对称点F,连接PF,则PE=PF,根据两点之间线段最短以及垂线段最短,得出当CF⊥AB时,PC+PE=PC+PF=CF(最短),最后根据勾股定理,求得CF的长即可得出PC+PE的最小值;
(2)根据轴对称的性质进行作图.方法1:作B关于AC的对称点E,连接DE并延长,交AC于P,连接BP,则∠APB=∠APD.方法2:作点D关于AC的对称点D',连接D'B并延长与AC的交于点P,连接DP,则∠APB=∠APD.
解答 解:(1)【解决问题】
如图②,作点E关于AD的对称点F,连接PF,则PE=PF,
当点F,P,C在一条直线上时,PC+PE=PC+PF=CF(最短),
当CF⊥AB时,CF最短,此时BF=$\frac{1}{2}$AB=3(cm),
∴Rt△BCF中,CF=$\sqrt{B{C}^{2}-B{F}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$(cm),
∴PC+PE的最小值为3$\sqrt{3}$cm,
故答案为:3$\sqrt{3}$;
(2)【拓展研究】
方法1:如图③,作B关于AC的对称点E,连接DE并延长,交AC于P,点P即为所求,连接BP,则∠APB=∠APD.
方法2:如图④,作点D关于AC的对称点D',连接D'B并延长与AC的交于点P,点P即为所求,连接DP,则∠APB=∠APD.
点评 本题属于轴对称-最短路线问题,本题考查了勾股定理、轴对称的性质,利用轴对称作图与基本作图等知识点的综合应用,熟知两点之间,线段最短以及垂线段最短是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,利用标杆BE测量建筑物DC的高度,如果标杆BE长为1.5米,测得AB=2米,BC=8米,且点A、E、D在一条直线上,则楼高CD是7.5米.
如图,利用标杆BE测量建筑物DC的高度,如果标杆BE长为1.5米,测得AB=2米,BC=8米,且点A、E、D在一条直线上,则楼高CD是7.5米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:
某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:| 成绩 | 划记 | 频数 | 频率 |
| 优秀 | 正正正 | a | 0.3 |
| 良好 | 正正正正正正 | 30 | b |
| 合格 | 正 | 9 | 0.15 |
| 不合格 |   | c | d |
| 合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com