
分析 (1)根据二次根式的乘法和除法可以解答本题;
(2)根据二次根式的除法可以解答本题;
(3)根据二次根式的乘法和除法可以解答本题;
(4)根据二次根式的乘法和除法可以解答本题;
(5)根据二次根式的加法和减法可以解答本题;
(6)根据二次根式的乘法和除法可以解答本题;
(7)根据完全平方公式和平方差公式可以解答本题;
(8)先化简括号内的式子,再根据乘法的分配律可以解答本题.
解答 解:(1)$-\sqrt{7}÷3\sqrt{\frac{14}{15}}×\frac{3}{2}\sqrt{2\frac{1}{2}}$
=$-\sqrt{7}×\frac{1}{3}\sqrt{\frac{15}{14}}×\frac{3}{2}\sqrt{\frac{5}{2}}$
=$\frac{1}{3}×\frac{3}{2}×\sqrt{7×\frac{15}{14}×\frac{5}{2}}$
=$\frac{5\sqrt{3}}{4}$;
(2)$2\sqrt{x{y^3}}÷({-\frac{1}{2}\sqrt{{x^3}{y^2}}})$
=-$2\sqrt{x{y}^{3}}×2\sqrt{\frac{1}{{x}^{3}{y}^{2}}}$
=-$\frac{4\sqrt{y}}{x}$;
(3)$\sqrt{4\frac{4}{5}}•3\sqrt{5}÷(-\frac{3}{4}\sqrt{10})$
=-$\sqrt{\frac{24}{5}}×3\sqrt{5}×\frac{4}{3}×\frac{1}{\sqrt{10}}$
=-$\frac{8\sqrt{15}}{5}$;
(4)$\sqrt{a{b^3}}÷({-3\sqrt{\frac{b}{2a}}})×({-3\sqrt{2a}})$
=$\sqrt{a{b}^{3}}×\frac{1}{3}\sqrt{\frac{2a}{b}}×3\sqrt{2a}$
=2ab$\sqrt{a}$;
(5)$\sqrt{24}+\sqrt{\frac{2}{3}}-3\sqrt{6}$
=$2\sqrt{6}+\frac{\sqrt{6}}{3}-3\sqrt{6}$
=$-\frac{2\sqrt{6}}{3}$;
(6)$\sqrt{30}×\frac{3}{2}\sqrt{2\frac{2}{3}}÷2\sqrt{2\frac{1}{2}}$
=$\sqrt{30}×\frac{3}{2}\sqrt{\frac{8}{3}}×\frac{1}{2}\sqrt{\frac{2}{5}}$
=3$\sqrt{2}$;
(7)${({\sqrt{5}-2})^2}+({\sqrt{5}-3})({\sqrt{5}+3})$
=5-4$\sqrt{5}$+4+5-9
=5-4$\sqrt{5}$;
(8)$(\frac{1}{3}\sqrt{27}-\sqrt{24}-3\sqrt{\frac{2}{3}})•\sqrt{12}$
=$(\sqrt{3}-2\sqrt{6}-\sqrt{6})•2\sqrt{3}$
=$(\sqrt{3}-3\sqrt{6})•2\sqrt{3}$
=6-18$\sqrt{2}$.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式的混合运算的计算方法.


科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5cm | B. | 4cm | C. | $\sqrt{7}$cm | D. | 5cm 或$\sqrt{7}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,每个小正方形的边长为1,△ABC的三个顶点都在格点(小正方形的顶点)上.
如图,每个小正方形的边长为1,△ABC的三个顶点都在格点(小正方形的顶点)上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请在括号内加注理由或在横线上填入相关内容:
请在括号内加注理由或在横线上填入相关内容:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 3,4,5 | 32+42=52 |
| 5,12,13, | 52+122=132 |
| 7,24,25 | 72+242=252 |
| 9,40,41 | 92+402=412 |
| … | … |
| 17,b,c | 172+b2=c2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
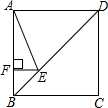 如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
如图,正方形ABCD的边长为8,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 8-4$\sqrt{2}$ | D. | 8$\sqrt{2}$-8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com