练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
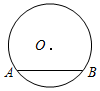
    6．如图，已知⊙O的半径为5，弦AB长度为8，则⊙O上到弦AB所在直线的距离为2的点有（　　）个．
    A．1B．2C．3D．4

    分析 连接OA，作OC⊥AB交AB于C，交⊙O于D，根据垂径定理求出AC，根据勾股定理求出OC，得到CD的长，比较即可得到答案．

    解答 解：连接OA，作OC⊥AB交AB于C，交⊙O于D，
    则AC=$\frac{1}{2}$AB=4，
    由勾股定理得，OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=3，
    则CD=2，
    故⊙O上到弦AB所在直线的距离为2的点有3个，
    故选：C．

    点评 本题考查的是垂径定理和勾股定理的应用，掌握垂直弦的直径平分这条弦，并且平分弦所对的两条弧是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．下列各式中，正确的是（　　）
    A．${3^{-2}}=-\frac{1}{9}$B．${（-3）^{-2}}=-\frac{1}{9}$C．${（-\frac{1}{3}）^{-2}}=9$D．${（-\frac{1}{3}）^{-2}}=-9$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

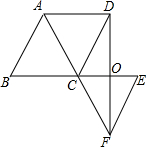    17．如图，延长?ABCD的边BC至点E，使CE=BC，连接AC并延长至点F，使CF=AC，连接EF、DF，DF交CE于O，求证：OD=OF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

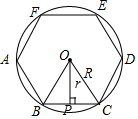    14．三正多边形的中心、半径、中心角、弦心距、边长之间的关系如图：请指出圆内接正六边形的中心、半径、中心角、弦心距．若设半径为R、弦心距为r，边长为a，则R、r、a之间有怎么的数量关系？周长、面积？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

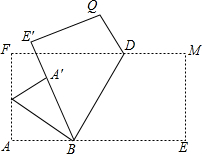    1．将一张长方形纸片的一角折叠，使点A落在A′处，BC为折痕，然后把BE折过去，使之与A′B重合，折痕为BD，那么两条折痕BC与BD的夹角是多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知，如图∠1和∠2是直线a，b被直线c截出的内错角，且∠1=∠2，求证：a∥b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图所示，四边形ABCD是一个边长为90米的正方形，甲在A处，乙在B处，两人同时出发，都沿A→B→C→D→A…的方向行走，甲每分钟走65米，乙每分钟走72米，则两人第一次相遇在正方形的哪条边上？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．阅读下面计算过程：
    $\frac{1}{\sqrt{2}+1}$=$\frac{1×（\sqrt{2}-1）}{（\sqrt{2}+1）（\sqrt{2}-1）}$=$\sqrt{2}$-1；
    $\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×（\sqrt{3}-\sqrt{2}）}{（\sqrt{3}+\sqrt{2}）（\sqrt{3}-\sqrt{2}）}$=$\sqrt{3}$-$\sqrt{2}$；
    $\frac{1}{\sqrt{5}+2}$=$\frac{1×（\sqrt{5}-2）}{（\sqrt{5}+2）（\sqrt{5}-2）}$=$\sqrt{5}$-2．
    求：（1）$\frac{1}{\sqrt{7}+\sqrt{6}}$的值．
    （2）$\frac{1}{\sqrt{n+1}+\sqrt{n}}$（n为正整数）的值．
    （3）$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{100}+\sqrt{99}}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知（y-z）2+（z-x）2+（x-y）2=（y+z-2x）2+（x+z-2y）2+（x+y-2z）2，求证：x=y=z．

    查看答案和解析>>

    同步练习册答案