
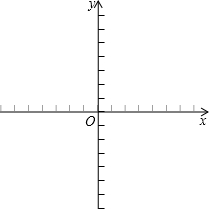
 已知抛物线y=-x2+4x+5与x轴的交点A,B(A在B的左边),顶点为P.
已知抛物线y=-x2+4x+5与x轴的交点A,B(A在B的左边),顶点为P.分析 (1)令y=0,求出A、B的坐标,然后求出AB的长度,再求出点P的坐标,求出△PAB的高,利用三角形的面积公式即可求出答案.
(2)过点Q作QC⊥x轴于点C,由S△QAB=30可知QC=10,设点Q(a,-a2+4a+5),根据QC=10列出方程求出a的值即可.
解答 解:(1)当y=0时得 0=-x2+4x+5
解得x=-1或x=5,
∴A(-1,0),B(5,0),
∴AB=6,
∵点P得坐标为(2,9)
∴S△PAB=$\frac{1}{2}$×6×9=27,
(2)过点Q作QC⊥x轴于点C,
设点Q(a,-a2+4a+5),
∴QC=|-a2+4a+5|,
∵S△QAB=30,
∴$\frac{1}{2}$AB•QC=30,
∴QC=10,
∴|-a2+4a+5|=10,
当-a2+4a+5=10时,
∵△=-4<0,
∴此方程无解,
当-a2+4a+5=-10时,
解得:a=2±$\sqrt{19}$,
∴Q的坐标为(2±$\sqrt{19}$,-10)
点评 本题考查二次函数与x轴的交点问题,涉及一元二次方程的解法,分类讨论的思想.


科目:初中数学 来源: 题型:选择题
| A. | k<5 | B. | k≥5,且k≠1 | C. | k≤5,且k≠1 | D. | k>5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 摸球的次数s | 150 | 300 | 600 | 900 | 1200 | 1500 |
| 摸到白球的频数n | 63 | a | 247 | 365 | 484 | 606 |
| 摸到白球的频率$\frac{n}{s}$ | 0.420 | 0.410 | 0.412 | 0.406 | 0.403 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠ABC=60°,∠C=70°,求∠DAC,∠BOA,∠EAD的度数.
如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠ABC=60°,∠C=70°,求∠DAC,∠BOA,∠EAD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
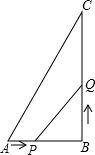 如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,设移动时间为t(s).
如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,设移动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com