
【题目】在![]() 中,
中,![]() ,以
,以![]() 为斜边作等腰直角三角形
为斜边作等腰直角三角形![]() ,且点
,且点![]() 与点
与点![]() 在直线
在直线![]() 的两侧,连接
的两侧,连接![]() .
.
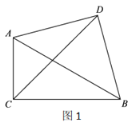
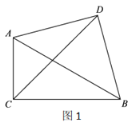
(1)如图1,若![]() ,则
,则![]() 的度数为______.
的度数为______.
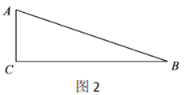
(2)已知![]() ,
,![]() .
.
①依题意将图2补全;
②求![]() 的长;
的长;
小聪通过观察、实验、提出猜想,与同学们进行交流,通过讨论,形成了求![]() 长的几种想法:
长的几种想法:
想法1:延长![]() ,在
,在![]() 延长线上截取
延长线上截取![]() ,连接
,连接![]() .要求
.要求![]() 的长,需证明
的长,需证明![]() ,
,![]() 为等腰直角三角形.
为等腰直角三角形.
想法2:过点![]() 作
作![]() 于点
于点![]() ,
,![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,要求
,要求![]() 的长,需证明
的长,需证明![]() ,
,![]() 为等腰直角三角形.
为等腰直角三角形.
……
请参考上面的想法,帮助小聪求出![]() 的长(一种方法即可).
的长(一种方法即可).
(3)用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系(直接写出即可).
之间的数量关系(直接写出即可).
【答案】(1)105度;(2)①将图2补全见解析;②![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求出∠CAB=60°,再利用等腰直角三角形求出∠BAD=45°,进而求出∠CAD;
(2)①根据题意及基本作图即可补全图形;延长![]() ,在
,在![]() 延长线上截取
延长线上截取![]() ,连接
,连接![]() .要求
.要求![]() 的长,需证明
的长,需证明![]() ,
,![]() 为等腰直角三角形再利用等腰直角三角形的性质即可得出解;
为等腰直角三角形再利用等腰直角三角形的性质即可得出解;
(3)同(2)的方法即可得出结论.
(1)∵![]() ,
,![]()
∴∠CAB=90°-∠ABC=60°
∵△![]() 是等腰直角三角形,
是等腰直角三角形,
∴∠BAD=45°
∴![]() =∠CAB+∠BAD=105°
=∠CAB+∠BAD=105°
故答案为:105°.
(2)①补全图形,如图2所示.
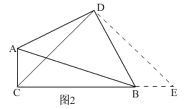
②延长![]() ,在
,在![]() 延长线上截取
延长线上截取![]() ,
,
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD=180°.
∵∠DBE+∠CBD=180°,
∴∠CAD=∠DBE.
∵DA=DB,AC=BE,
∴△ACD≌△BED.
∴DC=DE,∠ADC=∠BDE.
∴∠CDE=90°.
∴△CDE为等腰直角三角形.
∵AC=1,BC=3,
∴CE=4.
∵CE2=CD2+DE2,
∴42=CD2+CD2
∴CD=![]() .
.
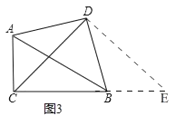
(3)AC+BC=![]() CD,
CD,
理由:如图3,延长![]() ,在
,在![]() 延长线上截取
延长线上截取![]() ,
,
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD=180°.
∵∠DBE+∠CBD=180°,
∴∠CAD=∠DBE.
∵DA=DB,AC=BE,
∴△ACD≌△BED.
∴DC=DE,∠ADC=∠BDE.
∴∠CDE=90°.
∴△CDE为等腰直角三角形.
∴CE2=CD2+DE2,
∴CE=![]() CD,
CD,
∵CE=BC+BE=BC+AC.
即:AC+BC=![]() CD.
CD.


 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:
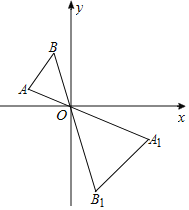
【题目】如图,已知△AOB和△A1OB1是以点O为位似中心的位似图形,且△AOB和△A1OB1的周长之比为1:2,点B的坐标为(-1,2),则点B1的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
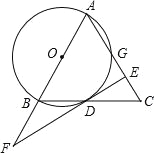
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于边D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.
(1)求证:BD=CD;
(2)若AE=6,BF=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着网络购物的盛行,“菜鸟驿站”新兴的代收快递业务越来越受到人们的青睐.“菜鸟驿站”某代收点只代收![]() ,
,![]() 两区的快递.4月份该代收点对
两区的快递.4月份该代收点对![]() ,
,![]() 两区代收数据进行统计,
两区代收数据进行统计,![]() 区比
区比![]() 区平均每个快递轻1千克.
区平均每个快递轻1千克.
(1)4月份第四周![]() 区共有300个快递,
区共有300个快递,![]() 区快递数为
区快递数为![]() 区的
区的![]() ,若本周该代收点的快递重量不低于1700千克,则
,若本周该代收点的快递重量不低于1700千克,则![]() 区该周平均每个快递至少重多少千克?
区该周平均每个快递至少重多少千克?
(2)随着夏季的到来,5月份第四周![]() 区快递数比4月份第四周增长了
区快递数比4月份第四周增长了![]() ,但
,但![]() 区平均每个快递比(1)中相应最少重量减少了
区平均每个快递比(1)中相应最少重量减少了![]() 千克,
千克,![]() 区快递数比4月份第四周增长了10%,平均每单比(1)中相应最少重量减少了
区快递数比4月份第四周增长了10%,平均每单比(1)中相应最少重量减少了![]() ,第四周两区快递总重量比第四周的最少重量减少了336千克,求
,第四周两区快递总重量比第四周的最少重量减少了336千克,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年初,新型冠状病毒肺炎侵袭湖北,武汉是重灾区,某爱心人士两次购买N95口罩支援武汉,第一次花了500000元,第二次花了770000,购买了同样的N95口罩,已知第二次购买的口罩的单价是第一次的1.4倍,且比第一次多购进了10000个,求该爱心人士第一次购进口罩的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
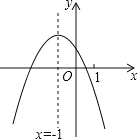
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小武新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小战和同学们一起到操场测量学校旗杆高度,他们首先在斜坡底部C地测得旗杆顶部A的仰角为45°,然后上到斜坡顶部D点处再测得旗杆顶部A点仰角为37°(身高忽略不计).已知斜坡CD坡度i=1:2.4,坡长为2.6米,旗杆AB所在旗台高度EF为1.4米,旗台底部、台阶底部、操场在同一水平面上.则请问旗杆自身高度AB为( )米.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
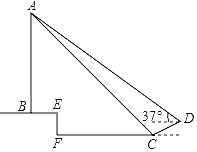
A.10.2B.9.8C.11.2D.10.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com