
【题目】现有两个不透明的乒乓球盒,甲盒中装有1个白球和2个红球,乙盒中装有2个白球和若干个红球,这些小球除颜色不同外,其余均相同.若从乙盒中随机摸出一个球,摸到红球的概率为![]() .
.
(1)求乙盒中红球的个数;
(2)若先从甲盒中随机摸出一个球,再从乙盒中随机摸出一个球,请用树形图或列表法求两次摸到不同颜色的球的概率.
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
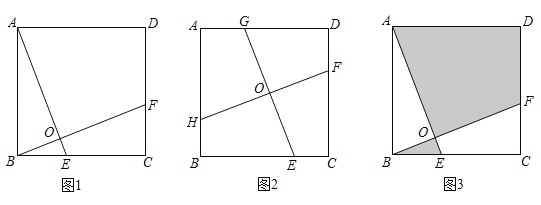
【题目】 在正方形ABCD中.
(1)如图1,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,试判断AE与BF的数量关系,并说明理由;
(2)如图2,点E、F、G、H分别在边BC、CD、DA、AB上,EG、FH相交于点O,∠GOH=90°,且EG=7,求FH的长;
(3)如图3,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,若AB=5,图中阴影部分的面积与正方形的面积之比为4:5,求△ABO的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分7分)已知关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使此方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为灾区开展了"献出我们的爱"赈灾捐款活动,九年级(1)班50名同学积极参加了这次赈灾捐款活动,
捐款(元) | 10 | 15 | 30 |
| 50 | 60 |
人数 | 3 | 6 | 11 |
| 13 | 6 |
因不慎,表中数据有两处被墨水污染,已无法看清,但已知全班平均每人捐款38元
(1)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程.
(2)该班捐款金额的众数,中位数分别是多少?
(3)如果用九年级(1)班捐款情况作为一个样本,请估计全校1200人中捐款在40元以上(包括40元)的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,对角线
,对角线![]() 绕点
绕点![]() 逆时针旋转,分别交边
逆时针旋转,分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
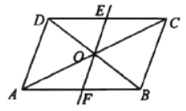
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() .当
.当![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() 时,判断四边形
时,判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=ax2+bx+c(a≠0),过(1,y1)(2,y2).
①若 y1>0 时,则 a+b+c>0
②若 a=b 时,则 y1<y2
③若 y1<0,y2>0,且 a+b<0,则 a>0
④若 b=2a﹣1,c=a﹣3,且 y1>0,则抛物线的顶点一定在第三象限上述四个判断正确的有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
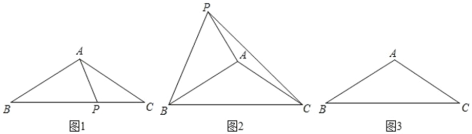
【题目】等腰△ABC 中,AB=AC,∠BAC=120°,点 P 为平面内一点.
(1)如图 1,当点 P 在边 BC 上时,且满足∠APC=120°,求![]() 的值;
的值;
(2)如图 2,当点 P 在△ABC 的外部,且满足∠APC+∠BPC=90°,求证:BP=![]() AP;
AP;
(3)如图 3,点 P 满足∠APC=60°,连接 BP,若 AP=1,PC=3,直接写出BP 的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
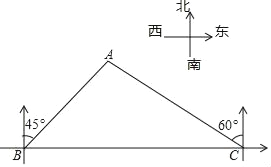
【题目】如图,一位旅行者骑自行车沿湖边正东方向笔直的公路BC行驶,在B地测得湖中小岛上某建筑物A在北偏东45°方向,行驶12min后到达C地,测得建筑物A在北偏西60°方向如果此旅行者的速度为10km/h,求建筑物A到公路BC的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形纸片![]() 的边长为
的边长为![]() 翻折
翻折![]() 使点
使点![]() 两点重合在对角线
两点重合在对角线![]() 上一点
上一点![]() 分别是折痕.设
分别是折痕.设![]() .
.
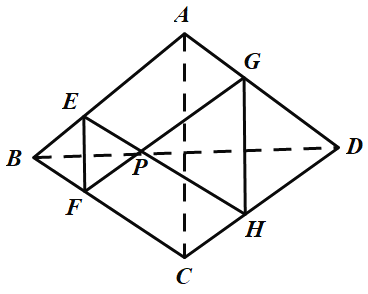
(1)证明:![]() ;
;
(2)当![]() 时,六边形
时,六边形![]() 周长的值是否会发生改变,请说明理由;
周长的值是否会发生改变,请说明理由;
(3)当![]() 时,六边形
时,六边形![]() 的面积可能等于
的面积可能等于![]() 吗?如果能,求此时
吗?如果能,求此时![]() 的值;如果不能,请说明理由.
的值;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com