
【题目】在平面直角坐标系中,直线y=k1x+b与x轴交于点B,与y轴交于点C,与反比例函数y=![]() 的图象在第一象限交于点A(3,1),连接OA.
的图象在第一象限交于点A(3,1),连接OA.
(1)求反比例函数y=![]() 的解析式;
的解析式;
(2)若S△AOB:S△BOC=1:2,求直线y=k1x+b的解析式.
【答案】(1)反比例函数的解析式为y=![]() ;(2)直线的解析式为y=x﹣2;(3)直线的解析式为y=﹣
;(2)直线的解析式为y=x﹣2;(3)直线的解析式为y=﹣![]() x+2.
x+2.
【解析】(1)将点A的坐标代入反比例函数解析式中,得出关于k2的一元一次方程,解方程即可得出结论;
(2)分两种情况考虑:①直线y=k1x+b经过第一、三、四象限,由S△AOB:S△BOC=1:2结合三角形的面积公式得出C的坐标,由待定系数法即可求出此时直线的函数解析式;②直线y=k1x+b经过第一、二、四象限,由S△AOB:S△BOC=1:2结合三角形的面积公式得出点C的坐标,由待定系数法即可求出此时直线的函数解析式.
解:(1)将点A(3,1)代入到y=![]() 中,得1=
中,得1=![]() ,解得:k2=3.
,解得:k2=3.
故反比例函数的解析式为y=![]() .
.
(2)符合题意有两种情况:①直线y=k1x+b经过第一、三、四象限,如图1所示.

∵S△AOB:S△BOC=1:2,点A(3,1),∴点C的坐标为(0,﹣2).
则有![]() ,解得:
,解得:![]() .
.
∴直线的解析式为y=x﹣2.
②直线y=k1x+b经过第一、二、四象限,如图2所示.
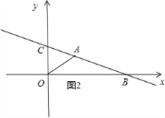
∵S△AOB:S△BOC=1:2,点A(3,1),∴点C的坐标为(0,2).
则有![]() ,解得:
,解得:![]() .
.
∴直线的解析式为y=﹣![]() x+2.
x+2.
“点睛”本题考查了反比例函数与一次函数交点的问题、待定系数法求函数解析式以及三角形的面积公式,解题的关键:(1)将点A的坐标代入反比例函数解析式中得到关于k2的一元一次方程;(2)分两种情况分别求出点C的坐标.本题属于基础题,难度不大,解决该题型题目时,结合点的坐标利用待定系数法求出函数解析式是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=8,将矩形沿AC折叠,点D落在点F处,AF与BC交于点E. 
(1)判断△AEC的形状,并说明理由;
(2)求△AEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:

(1)∵________=__________(已知)
∴AB∥CD(同位角相等,两条直线平行)
(2)∵_________=__________(已知)
∴AB∥CD(内位角相等,两条直线平行)
(3)∵_________+_________=180(已知)
∴AB∥CD(同旁内角互补,两条直线平行)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y与x﹣2成正比例,当x=3时,y=2.
(1)求y与x之间的函数关系式;
(2)当﹣2<x<3时,求y的范围.
(3)证明:△ABC是直角三角形.
(4)请求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB. 
(1)求证:四边形PMAN是正方形;
(2)求证:EM=BN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”,黄冈市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计黄冈市直机关500户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com