
【题目】如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M;
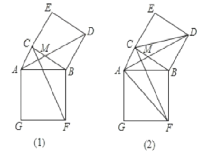
(1)求证:△ABD≌△FBC;
(2) 如图(2),已知AD=6,求四边形AFDC的面积;
【答案】(1)见解析;(2)18.
【解析】
(1)根据四边形ABFG、BCED是正方形得到两对边相等,一对直角相等,根据图形利用等式的性质得到一对角相等,利用SAS即可得到三角形全等;
(2)连接FD,由(1)的三角形全等,得到AD=FC,∠BAD=∠BFC,利用等式的性质及垂直定义得到AD与CF垂直,四边形AFDC面积=三角形ACD面积+三角形ACF面积+三角形DMF面积-三角形ACM面积,求出即可;
(1)∵四边形ABFG、BCED是正方形,
∴AB=FB,CB=DB,∠ABF=∠CBD=90°,
∴∠ABF+∠ABC=∠CBD+∠ABC,
即∠ABD=∠CBF,
在△ABD和△FBC中,
 ,
,
∴△ABD≌△FBC(SAS);
(2)连接FD,设CF与AB交于点N,
∵△ABD≌△FBC,
∴AD=FC,∠BAD=∠BFC,
∴∠AMF=180°∠BAD∠CNA=180°(∠BFC+∠BNF)=180°90°=90°,
∴AD⊥CF,
∵AD=6,
∴FC=AD=6,
∴S![]() =S
=S![]() +S
+S![]() +S
+S![]() S
S![]() ,
,
=![]() ADCM+
ADCM+![]() CFAM+
CFAM+![]() DMFM
DMFM![]() AMCM,
AMCM,
=3CM+3AM+![]() (6AM)(6CM)
(6AM)(6CM) ![]() AMCM=18;
AMCM=18;


科目:初中数学 来源: 题型:
【题目】如图∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.
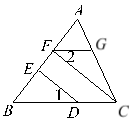
证明:∵CF⊥AB,DE⊥AB (已知)
∴∠BED=90°,∠BFC=90°( )
∴∠BED=∠BFC ( )
∴ED∥FC ( )
∴∠1=∠BCF ( )
∵∠2=∠1 ( 已知 )
∴∠2=∠BCF ( )
∴FG∥BC ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铜梁永辉商场今年二月份以每桶40元的单价购进1000桶甲、乙两种食用油,然后以甲种食用油每桶75元、乙桶食用油每桶60元的价格售完,共获利29000元.
(1)求该商场分别购进甲、乙两种食用油多少桶?
(2)为了增加销售量,获得最大利润,根据销售情况和市场分析,在进价不变的情况下该经销商决定调整价格,将甲种食用油的价格在二月份的基础上下调20%,乙种食用油的价格上涨![]() a%,但甲的销售量还是较二月下降了
a%,但甲的销售量还是较二月下降了![]() a%,而乙的销售量却上升了25%,结果三月份的销售额比二月份增加了1000元,求a的值.
a%,而乙的销售量却上升了25%,结果三月份的销售额比二月份增加了1000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如右图所示,图象过点(-1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(-2,y1),点B(,y2),点C(,y3)在该函数图象上,则y1<y3<y2;其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点![]() 开始沿东西方向的直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿东西方向的直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]()
(1)蜗牛最后是否回到出发点?请说明理由;
(2)蜗牛离开出发点![]() 最远时是_______厘米;
最远时是_______厘米;
(3)在爬行过程中,如果蜗牛每爬2厘米奖励一粒芝麻,求蜗牛-共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数 y=kx+b 的图像与反比例函数 y=![]() 的图像交于 A(-2,1),B(1,n)两点,
的图像交于 A(-2,1),B(1,n)两点,
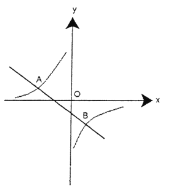
(1)求反比例函数和一次函数的表达式;
(2)求使一次函数的值大于反比例函数的值时 x 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边上的高,连接
边上的高,连接![]() ,过点
,过点![]() 作
作![]() 与点
与点![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,
,![]() .
.
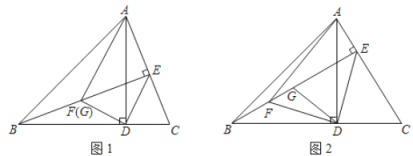
(1)如图![]() ,若点
,若点![]() 与点
与点![]() 重合,求证:
重合,求证:![]() ;
;
(2)如图![]() ,请写出
,请写出![]() 与
与![]() 之间的关系并证明.
之间的关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 的图象如图所示,则结论:①两函数图象的交点
的图象如图所示,则结论:①两函数图象的交点![]() 的坐标为(2,2);②当x>2时,
的坐标为(2,2);②当x>2时,![]() ;③当x=1时,BC=3;④当x逐渐增大时,
;③当x=1时,BC=3;④当x逐渐增大时,![]() 随着
随着![]() 的增大而增大,
的增大而增大,![]() 随着
随着![]() 的增大而减小.则其中正确结论的序号是( )
的增大而减小.则其中正确结论的序号是( )
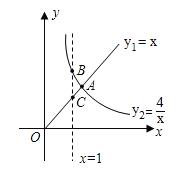
A.①②B.①③C.②④D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com