
【题目】在平面直角坐标系xOy中,直线y=x+2经过点A(m,-2),将点A向右平移7个单位长度,得到点B,抛物线![]() 的顶点为C.
的顶点为C.
(1)求m的值和点B的坐标;
(2)求点C的坐标(用含n的代数式表示);
(3)若抛物线与线段AB只有一个公共点,结合函数图象,求n的取值范围.
【答案】(1)m=-4,B(3,-2);(2)C(2,1-4n);(3)n≤![]() 或n=
或n=![]() 或n>1.
或n>1.
【解析】
(1)根据直线 y=x+2 经过点 A(m,-2)可求点A的坐标,根据平移的性质可求点B的坐标;
(2)将二次函数解析式用配方法变形为顶点式即可求出C点坐标;
(3)结合图形,分三种情况:①n>0;②n<0,③抛物线的顶点在线段BC上;进行讨论即可求解.
解:(1)∵直线 y=x+2 经过点 A(m,-2),
∴m+2=-2,
∴m=-4,
∵将点 A(-4,-2) 向右平移7个单位长度,得到点B,
∴B点坐标为(3,-2)
(2)![]() ,
,
∴![]()
∴![]()
∴![]()
∴抛物线![]() 的顶点为C为(2,1-4n)
的顶点为C为(2,1-4n)
(3)又(2)可知抛物线对称轴为x=2, 顶点C为(2,1-4n),点(3,1-3n)、(-4,1+32n)
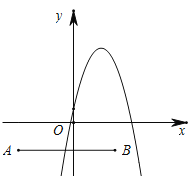
当n<0时,抛物线顶点C为(2,1-4n)、(3,1-3n),在B在抛物线下方,右侧无交点,
∴A在抛物线上方,即:1+32n≤-2,
∴n≤![]()
当n>0时,若抛物线顶点在AB上,如图:
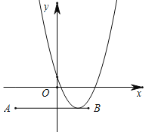
即1-4n=-2, n=![]() ,
,
当n>0时,若抛物线顶点在AB下方,而点B在抛物线下方,点A在抛物线下方,
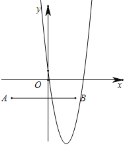
即: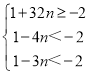 ,
,
∴ n>1
故当n≤![]() 或n=
或n=![]() 或n>1时,若抛物线与线段AB只有一个公共点,
或n>1时,若抛物线与线段AB只有一个公共点,


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,D、E分别是斜边AB、直角边BC上的点,把
,D、E分别是斜边AB、直角边BC上的点,把![]() 沿着直线DE折叠.
沿着直线DE折叠.

![]() 如图1,当折叠后点B和点A重合时,用直尺和圆规作出直线DE;
如图1,当折叠后点B和点A重合时,用直尺和圆规作出直线DE;![]() 不写作法和证明,保留作图痕迹
不写作法和证明,保留作图痕迹![]()
![]() 如图2,当折叠后点B落在AC边上点P处,且四边形PEBD是菱形时,求折痕DE的长.
如图2,当折叠后点B落在AC边上点P处,且四边形PEBD是菱形时,求折痕DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
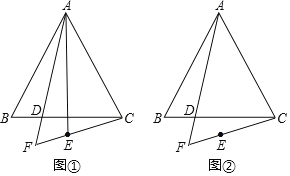
【题目】在等边△ABC中,点D是边BC上一点.作射线AD,点B关于射线AD的对称点为点E.连接CE并延长,交射线AD于点F.
(1)如图①,连接AE,
①AE与AC的数量关系是 ;
②设∠BAF=a,用a表示∠BCF的大小;
(2)如图②,用等式表示线段AF,CF,EF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划投资![]() 万元引进一条汽车配件流水生产线,经过调研知道该流水生产线的年产量为
万元引进一条汽车配件流水生产线,经过调研知道该流水生产线的年产量为![]() 件,每件总成本为
件,每件总成本为![]() 万元,每件出厂价
万元,每件出厂价![]() 万元;流水生产线投产后,从第
万元;流水生产线投产后,从第![]() 年到第
年到第![]() 年的维修、保养费用累计
年的维修、保养费用累计![]() (万元)如下表:
(万元)如下表:
第 |
|
|
|
|
|
| ··· |
维修、保养费用累计 |
|
|
|
|
|
| ··· |
若上表中第![]() 年的维修、保养费用累计
年的维修、保养费用累计![]() (万元)与
(万元)与![]() 的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个.
的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个.
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)投产第几年该公司可收回![]() 万元的投资?
万元的投资?
(3)投产多少年后,该流水线要报废(规定当年的盈利不大于维修、保养费用累计即报费)?
查看答案和解析>>
科目:初中数学 来源: 题型:
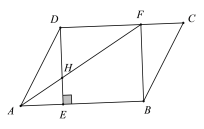
【题目】在平行四边形 ABCD 中,过点 D 作 DE⊥AB 于点 E,点 F 在 CD 上,CF =AE,连接 BF,AF.
(1)求证:四边形 BFDE 是矩形;
(2)若 AF 平分∠BAD,交DE与H点,且 AB=3AE,BF=6,求AH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
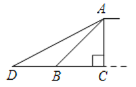
【题目】某市为了缓解城市交通压力,决定修建人行天桥,原设计天桥的楼梯与地面的夹角为45°(∠ABC=45°),BC=4.2 m,后考虑安全因素,将楼梯角B移到CB的延长线上点D处,使∠ADC=23°(如图所示).求BD的长(精确到0.1 m).(参考数据:sin 67°≈0.92,cos 67°≈0.39,tan 67°≈2.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1长为半径画弧,交直线y=![]() x于点B1.过点B1作B1A2∥y轴交直线y=2x于点A2,以O为圆心,OA2长为半径画弧,交直线y═
x于点B1.过点B1作B1A2∥y轴交直线y=2x于点A2,以O为圆心,OA2长为半径画弧,交直线y═![]() x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3,以点O为圆心,OA3长为半径画弧,交直线y=
x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3,以点O为圆心,OA3长为半径画弧,交直线y=![]() x于点B3;……按如此规律进行下去,点B2020的坐标为_____.
x于点B3;……按如此规律进行下去,点B2020的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣m)2+2m(m≠0)经过原点,其顶点为P,与x轴的另一交点为A.
(1)P点坐标为 ,A点坐标为 ;(用含m的代数式表示)
(2)求出a,m之间的关系式;
(3)当m>0时,若抛物线y=a(x﹣m)2+2m向下平移m个单位长度后经过点(1,1),求此抛物线的表达式;
(4)若抛物线y=a(x﹣m)2+2m向下平移|m|个单位长度后与x轴所截的线段长,与平移前相比有什么变化?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
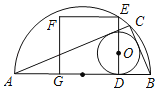
【题目】如图,AB为半圆的直径,C是半圆弧上一点,正方形DEFG的一边DG在直径AB上,另一边DE过△ABC的内切圆圆心O,且点E在半圆上.
(1)当正方形的顶点F也在半圆弧上时,半圆的半径与正方形边长的比为 ;
(2)当正方形DEFG的面积为100,且△ABC的内切圆⊙O的半径r=4,求半圆的直径AB的值;
(3)若半圆的半径为R,直接写出⊙O半径r可取得的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com