
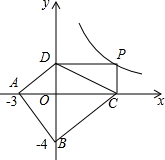
 如图,已知A(-3,0),B(0,-4),P为反比例函数y=$\frac{12}{x}$(x>0)图象上的动点,PC⊥x轴于C,PD⊥y轴于D,则四边形ABCD面积的最小值为( )
如图,已知A(-3,0),B(0,-4),P为反比例函数y=$\frac{12}{x}$(x>0)图象上的动点,PC⊥x轴于C,PD⊥y轴于D,则四边形ABCD面积的最小值为( )| A. | 12 | B. | 13 | C. | 24 | D. | 26 |
分析 设P点坐标为(x,$\frac{12}{x}$),将四边形分割为四个三角形,四边形ABCD面积的最小,即S△AOB+S△AOD+S△DOC+S△BOC最小.
解答 解:设P点坐标为(x,$\frac{12}{x}$),x>0,
则S△AOD=$\frac{1}{2}$×|-3|×|$\frac{12}{x}$|=$\frac{18}{x}$,S△DOC=$\frac{12}{2}$=6,
S△BOC=$\frac{1}{2}$×|-4|×|x|=2x,S△AOB=$\frac{1}{2}$×3×4=6.
∴S△AOB+S△AOD+S△DOC+S△BOC
=12+2x+$\frac{18}{x}$
=12+2(x+$\frac{9}{x}$)≥12+2×2×$\sqrt{\frac{x•9}{x}}$=24.
故选C.
点评 本题考查了反比例函数系数k的几何意义,三角形的面积,本题借用考查四边形面积的最小值来考查反比例函数图象的应用,综合能力较强.


科目:初中数学 来源: 题型:填空题
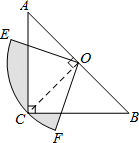 如图,在△ABC中∠C=90°,AC=BC=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为$\frac{1}{2}$π-1.
如图,在△ABC中∠C=90°,AC=BC=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为$\frac{1}{2}$π-1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
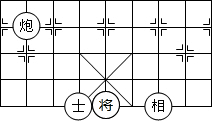 中国象棋在中国有着三千多年的历史,它难易适中,趣味性强,变化丰富细腻,棋盘棋子文字都体现了中国文化.如图,如果
中国象棋在中国有着三千多年的历史,它难易适中,趣味性强,变化丰富细腻,棋盘棋子文字都体现了中国文化.如图,如果 所在位置的坐标为(-1,-1),
所在位置的坐标为(-1,-1), 所在位置的坐标为(2,-1),那么,
所在位置的坐标为(2,-1),那么, 所在位置的坐标为(-3,2).
所在位置的坐标为(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
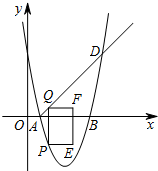 如图,在平面直角坐标系中,抛物线y=ax2+bx+5与x轴交于A(1,0)、B(5,0)两点,点D是抛物线上横坐标为6的点.点P在这条抛物线上,且不与A、D两点重合,过点P作y轴的平行线与射线AD交于点Q,过点Q作QF垂直于y轴,点F在点Q的右侧,且QF=2,以QF、QP为邻边作矩形QPEF.设矩形QPEF的周长为d,点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=ax2+bx+5与x轴交于A(1,0)、B(5,0)两点,点D是抛物线上横坐标为6的点.点P在这条抛物线上,且不与A、D两点重合,过点P作y轴的平行线与射线AD交于点Q,过点Q作QF垂直于y轴,点F在点Q的右侧,且QF=2,以QF、QP为邻边作矩形QPEF.设矩形QPEF的周长为d,点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
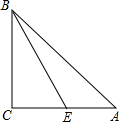 已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).
已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com