
【题目】如图1,平面直角坐标系中,直线y=kx+b与x轴交于点A(6,0),与y轴交于点B,与直线y=2x交于点C(a,4).
(1)求点C的坐标及直线AB的表达式;
(2)如图2,在(1)的条件下,过点E作直线l⊥x轴于点E,交直线y=2x于点F,交直线y=kx+b于点G,若点E的坐标是(4,0).
①求△CGF的面积;
②直线l上是否存在点P,使OP+BP的值最小?若存在,直接写出点P的坐标;若不存在,说明理由;
(3)若(2)中的点E是x轴上的一个动点,点E的横坐标为m(m>0),当点E在x轴上运动时,探究下列问题:
当m取何值时,直线l上存在点Q,使得以A,C,Q为顶点的三角形与△AOC全等?请直接写出相应的m的值.

【答案】(1)y=﹣x+6;(2)①6;②P(4,3);(3)A题:m的值为2或6或8.B题:m的值为3或6或![]() 或
或![]() .
.
【解析】
(1)将C(2,4)和A(6,0)代入y=kx+b,即可得到直线AB的解析式;
(2)①设点F(4,y1),G(4,y2),分别代入y=2x和y=-x+6,可得FE=8,GE=2,FG=6,过点C作CH⊥FG于H,依据S△FCG=![]() FG×CH,进行计算即可;②设点O关于直线l的对称点为D(8,0),设直线BD的解析式为y=mx+n,将B(0,6),D(8,0)代入y=mx+n,可得直线BD的解析式为y=-
FG×CH,进行计算即可;②设点O关于直线l的对称点为D(8,0),设直线BD的解析式为y=mx+n,将B(0,6),D(8,0)代入y=mx+n,可得直线BD的解析式为y=-![]() x+6,令x=4,则y=3,即可得出P(4,3);
x+6,令x=4,则y=3,即可得出P(4,3);
(3)选A题时,需要分数轴情况进行讨论,画出图形,依据全等三角形的对应顶点的位置,即可得到m的值;选B题时,依据△BFG是等腰三角形分四种情况进行讨论,进而得出m的值.
(1)将点C(a,4)代入y=2x,可得a=2,
∴C(2,4),
将C(2,4)和A(6,0)代入y=kx+b,可得
![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣x+6;
(2)①如图1,∵l⊥x轴,点E,F,G都在直线l上,且点E的坐标为(4,0),
∴点F,G的横坐标均为4,
设点F(4,y1),G(4,y2),分别代入y=2x和y=﹣x+6,可得
y1=8,y2=2,
∴F(4,8),G(4,2),
∴FE=8,GE=2,FG=6,
如图2,过点C作CH⊥FG于H,

∵C(2,4),
∴CH=4﹣2=2,
∴S△FCG=![]() FG×CH=
FG×CH=![]() ×6×2=6;
×6×2=6;
②存在点P(4,3),使得BP+OP的值最小.
理由:设点O关于直线l的对称点为D(8,0),
设直线BD的解析式为y=mx+n,
将B(0,6),D(8,0)代入y=mx+n,可得
![]() ,解得
,解得 ,
,
∴直线BD的解析式为y=﹣![]() x+6,
x+6,
点P在直线l:x=4上,令x=4,则y=3,
∴P(4,3);
(3)A题:m的值为2或6或8.
理由:分三种情况讨论:
①当△OAC≌△QCA,点Q在第四象限时,∠ECA=∠EAC,
∴AE=CE=4,OE=6﹣4=2,
∴m=2;

②当△ACO≌△ACQ,Q在第一象限时,OE=AO=6,
∴m=6;

③当△ACO≌△CAQ,点Q在第四象限时,四边形AOCQ是平行四边形,CQ=AO=6,AE=2,
∴OE=8,
∴m=8;

B题:m的值为3或6或![]() 或
或![]() .
.
理由:分四种情况讨论:
①如图,当BG=GF时,![]() m=﹣m+6﹣2m,
m=﹣m+6﹣2m,
解得m=![]() ;
;

②如图,当BF=GF时,m=2m﹣(﹣m+6),
解得m=3;

③如图,当GB=GF时,![]() m=2m﹣(﹣m+6),
m=2m﹣(﹣m+6),
解得m=![]() ;
;

④如图,当BG=BF时,FG=![]() BG,即2m﹣(﹣m+6)=
BG,即2m﹣(﹣m+6)=![]() ×
×![]() m,
m,
解得m=6.


科目:初中数学 来源: 题型:
【题目】尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图只需在⊙O上任取点A,从点A开始,以⊙O的半径为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是( ) ①两等分 ②三等分 ③四等分 ④五等分.
A.②
B.①②
C.①②③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,H,G,N在同一直线上,△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边.在△NMH中,MH是最长边.已知EF=2.1 cm,EH=1.1 cm,HN=3.3 cm.
(1)写出其他对应边及对应角;
(2)求线段MN及线段HG的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB>AC , 分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N , 作直线MN交AB于点D;连结CD.若AB=7,AC=5,则△ACD的周长为( )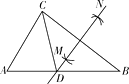
A.2 ![]()
B.12
C.17
D.19
查看答案和解析>>
科目:初中数学 来源: 题型:
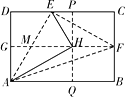
【题目】如图,矩形纸片ABCD中,G、F分别为AD、BC的中点,将纸片折叠,使D点落在GF上,得到△HAE , 再过H点折叠纸片,使B点落在直线AB上,折痕为PQ.连接AF、EF , 已知HE=HF.下列结论:①△MEH为等边三角形;②AE⊥EF;③△PHE∽△HAE;④![]() ,
, 
其中正确的结论是
A.①②③
B.①②④
C.①③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴的正半轴上,BC=2AC , 点B、C在反比例函数y= ![]() (x>0)的图象上,则△OAB的面积为.
(x>0)的图象上,则△OAB的面积为.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面算式,解答问题:
![]()
![]()
![]() ……
……
(1)请求出1 3 5 7 9 11的结果为 ;
请求出1 3 5 7 9 29 的结果为 ;
(2)若n 表示正整数,请用含 n 的代数式表示1 3 5 7 9 (2n 1) (2n 1) 的值为
(3)请用上述规律计算: 41 43 45 77 79 的值(要求写出详细解答过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com