
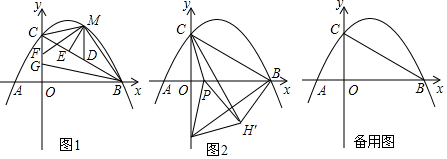
 .
. 分析 (1)利用待定系数法,把问题转化为方程组解决即可.
(2)如图1中,延长MD交c轴于H.首先证明△DEM是含有30度角的特殊直角三角形,DM最大时,△DME的周长最大,构建二次函数求出点M的坐标,将点B向上平移$\frac{\sqrt{3}}{2}$个单位得到点P(6,$\frac{\sqrt{3}}{2}$),作点P关于y轴的对称点P′(-6,$\frac{\sqrt{3}}{2}$),连接P′M交y轴于F,此时四边形BGFM的周长最小.
(3)分四种情形讨论①如图3中,当HH′=BH′时,②如图4中,当PH=PH′时,③如图5中,当HB=HH′时,④如图6中,当HH′=BH′时,分别求出OP的长即可解决问题.
解答 解:(1)∵抛物线y=-$\frac{\sqrt{3}}{6}$x2+bx+c与x轴交于A(-2,0)、B(6,0),
∴抛物线的解析式为抛物线y=-$\frac{\sqrt{3}}{6}$(x+2)(x-6)=-$\frac{\sqrt{3}}{6}$x2+$\frac{2}{3}$$\sqrt{3}$x+2$\sqrt{3}$.
∴C(0,2$\sqrt{3}$),
设直线BC的解析式为y=kx+b则有$\left\{\begin{array}{l}{b=2\sqrt{3}}\\{6k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=2\sqrt{3}}\end{array}\right.$,
∴直线BC的解析式为y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$.
(2)如图1中,延长MD交c轴于H.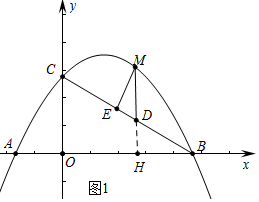
∵tan∠CBO=$\frac{CO}{BO}$=$\frac{\sqrt{3}}{3}$,
∴∠CBO=30°,
∵MH⊥OB,
∴∠BHD=90°,
∴∠BDH=∠EDM=60°,
∵ME⊥BC,
∴∠EMD=30°,
∴当DM的值最大时,△EMD的周长最大,设M(m,-$\frac{\sqrt{3}}{6}$m2+$\frac{2}{3}$$\sqrt{3}$m+2$\sqrt{3}$)则D(m,-$\frac{\sqrt{3}}{3}$m+2$\sqrt{3}$),
∴MD=-$\frac{\sqrt{3}}{6}$m2+$\frac{2}{3}$$\sqrt{3}$m+2$\sqrt{3}$+$\frac{\sqrt{3}}{3}$m-2$\sqrt{3}$=-$\frac{\sqrt{3}}{6}$m2+$\sqrt{3}$m=-$\frac{\sqrt{3}}{6}$(m-3)2+$\frac{3\sqrt{3}}{2}$,
∵-$\frac{\sqrt{3}}{6}$<0,
∴m=3时,MD有最大值,此时点M(3,$\frac{5\sqrt{3}}{2}$).
如图2中,∵点F(0,a+$\frac{\sqrt{3}}{2}$),G(0,a),∴FG=$\frac{\sqrt{3}}{2}$.
将点B向上平移$\frac{\sqrt{3}}{2}$个单位得到点P(6,$\frac{\sqrt{3}}{2}$),作点P关于y轴的对称点P′(-6,$\frac{\sqrt{3}}{2}$),连接P′M交y轴于F,此时四边形BGFM的周长最小.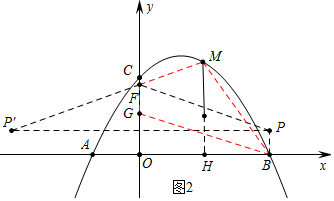
∵直线P′M的解析式为y=$\frac{2}{9}$$\sqrt{3}$x+$\frac{11}{6}$$\sqrt{3}$,
∴F(0,$\frac{11}{6}$$\sqrt{3}$),
∴四边形BGFM的周长最小值=BG+FG+FM+BM=PF+FG+FM+BM=P′F+FM+FG+BM=P′M+FG+BM=$\sqrt{93}$+$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{111}}{2}$.
(3)①如图3中,当HH′=BH′时,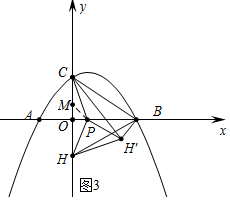
易知∠HCH′=∠H′CB=30°,
∴∠PCO=∠PCH′=15°,在OC上取一点M,使得CM=PM,则∠PMO=30°,设OP=x,则PM=CM=2x,OM=$\sqrt{3}$x,
则有2x+$\sqrt{3}$x=2$\sqrt{3}$,
∴x=4$\sqrt{3}$-6,
∴P(4$\sqrt{3}$-6,0).
②如图4中,当PH=PH′时,易知点P与点B重合,此时P(6,0).
③如图5中,当HB=HH′时,易知点H′在x轴上.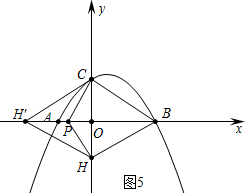
易知∠PCO=30°,OP=OC•tan30°=2,此时P(-2,0).
④如图6中,当HH′=BH′时,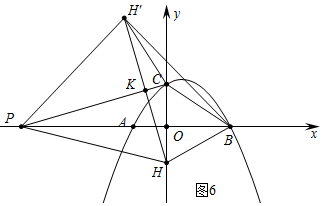
易知∠CHH′=∠CH′H=15°,
∵PH′=PH,CH′=CH,
∴PC⊥HH′于K,
∴∠CPO+∠PCO=90°,∵∠HCK=75°,
∴∠CPO=15°,
在OP上取一点Q,使得PQ=CQ,则∠CQO=30°,PQ=CQ=2OC=4$\sqrt{3}$,OQ=$\sqrt{3}$CO=6,
∴OP=4$\sqrt{3}$+6,
∴P(-4$\sqrt{3}$-6,0).
综上所述,满足条件的点P的坐标为(4$\sqrt{3}$-6,0)或(6,0)或(-2,0)或(-4$\sqrt{3}$-6,0).
点评 本题考查二次函数综合题、最值问题、轴对称最短问题、一次函数的应用、等腰三角形的判定和性质等知识,解题的关键是学会用转化的思想思考问题,学会构建二次函数解决最值问题,学会利用对称解决最短问题,本题体现了分类讨论的数学思想,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
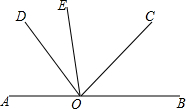 如图,已知,A、O、B在同一条线上,∠AOE=∠COD,∠EOD=30°.
如图,已知,A、O、B在同一条线上,∠AOE=∠COD,∠EOD=30°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知点A、B、C、D、E、F是半径为r的⊙O的六等分点,分别以A、D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )
已知点A、B、C、D、E、F是半径为r的⊙O的六等分点,分别以A、D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )| A. | ①④ | B. | ②③ | C. | ③④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a>0,b>0,则a+b>0 | B. | 对顶角相等 | ||
| C. | 全等三角形的对应角相等 | D. | 平行四边形的两组对边分别相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com