
【题目】 定义:在凸四边形中,我们把两组对边乘积的和等于对角线的乘积的四边形称为“完美四边形”
(1)在正方形、矩形、菱形中,一定是“完美四边形”的是______.
(2)如图1,在△ABC中,AB=2,BC=![]() ,AC=3,D为平面内一点,以A、B、C、D四点为顶点构成的四边形为“完美四边形”,若DA,DC的长是关于x的一元二次方程x2-(m+3)x+
,AC=3,D为平面内一点,以A、B、C、D四点为顶点构成的四边形为“完美四边形”,若DA,DC的长是关于x的一元二次方程x2-(m+3)x+![]() (5m2-2m+13)=0(其中m为常数)的两个根,求线段BD的长度.
(5m2-2m+13)=0(其中m为常数)的两个根,求线段BD的长度.
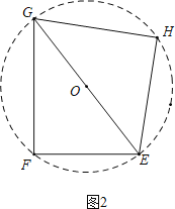
(3)如图2,在“完美四边形”EFGH中,∠F=90°,EF=6,FG=8,求“完美四边形”EFGH面积的最大值.
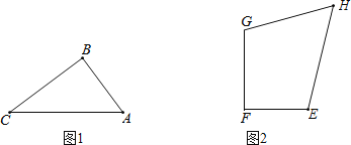
【答案】(1)正方形、矩形;(2)3;(3)49.
【解析】
(1)根据“完美四边形”的定义即可判断.
(2)利用一元二次方程的根的判别式求出m的值,推出AD=DC=2,判断出点D的位置即可解决问题.
(3)由完美四边形的定义以及托勒密定理的逆定理可知:四边形EFGH是圆的内接四边形,圆心是EC的中点O.当点H是![]() 的中点时,△EGH的面积最大,此时四边形EFGH的面积最大.
的中点时,△EGH的面积最大,此时四边形EFGH的面积最大.
解:(1)根据完美四边形的定义,可知“正方形”、“矩形”是完美四边形.
故答案为:“正方形”、“矩形”.
(2)∵关于x的一元二次方程x2-(m+3)x+![]() (5m2-2m+13)=0,有实数根,
(5m2-2m+13)=0,有实数根,
∴△=(m+3)2-4×![]() (5m2-2m+13)=-4(m-1)2≥0,
(5m2-2m+13)=-4(m-1)2≥0,
∴m=1,△=0,
∴方程为:x2-4x+4=0,
∴x1=x2=2,
∴AD=DC=2,
当点D在AC的下方,如图1中,
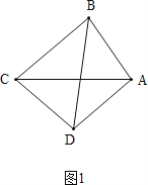
∵四边形ABCD是完美四边形,
∴BDAC=CDAB+BCAD,
∴3BD=4+5,
∴BD=3.
当点D在AC上方时,点D在线段BC上,不符合题意.
∴满足条件的BD的长为3;
(3)如图2中,
由完美四边形的定义以及托勒密定理的逆定理可知:四边形EFGH是圆的内接四边形,圆心是EC的中点O.
∵∠EFG=90°,EF=6,FG=8,
∴EG=![]() =10,
=10,
当点H是![]() 的中点时,△EGH的面积最大,此时四边形EFGH的面积最大,
的中点时,△EGH的面积最大,此时四边形EFGH的面积最大,
∴HG=HE=5![]() ,
,
∴四边形的面积的最大值=![]() ×6×8+
×6×8+![]() ×5
×5![]() ×5
×5![]() =49.
=49.


科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,
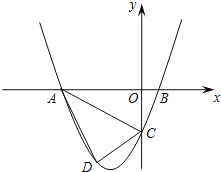
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是圆上一点,弦CD⊥AB于点E,且DC=AD.过点A作⊙O的切线,过点C作DA的平行线,两直线交于点F,FC的延长线交AB的延长线于点G.
(1)求证:FG与⊙O相切;
(2)连接EF,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市倡导垃圾分类投放,将日常垃圾分成四类,分别投放四种不同颜色的垃圾桶中,在“垃圾分类”模拟活动中,某同学把两个不同类的垃圾随意放入两个不同颜色的垃圾筒中,则这个同学正确分类投放垃圾的概率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
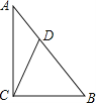
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,cosA=![]() ,点D是斜边AB上的动点且不与A,B重合,连接CD,点B'与点B关于直线CD对称,连接B'D,当B'D垂直于Rt△ABC的直角边时,BD的长为______.
,点D是斜边AB上的动点且不与A,B重合,连接CD,点B'与点B关于直线CD对称,连接B'D,当B'D垂直于Rt△ABC的直角边时,BD的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
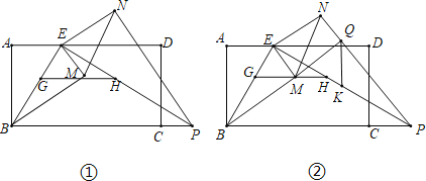
【题目】如图①,在矩形ABCD中,AB=![]() ,AD=3,点E是边AD靠近A的三等分点,点P是BC延长线上一点,且EP⊥EB,点G是BE上任意一点,过G作GH∥BP,交EP于点H.将△EGH绕点E逆时针旋转α(0<α<90°),得到△EMN(M、N分别是G、H的对应点).
,AD=3,点E是边AD靠近A的三等分点,点P是BC延长线上一点,且EP⊥EB,点G是BE上任意一点,过G作GH∥BP,交EP于点H.将△EGH绕点E逆时针旋转α(0<α<90°),得到△EMN(M、N分别是G、H的对应点).
(1)求BP的长;
(2)求![]() 的值;
的值;
(3)如图②当α=60°时,点M恰好落在GH上,延长BM交NP于点Q,取EP的中点K,连接QK.若点G在线段EB上运动,问QK是否有最小值?若有最小值,请求出点G运动到EB的什么位置时,QK有最小值及最小值是多少,若没有最小值,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
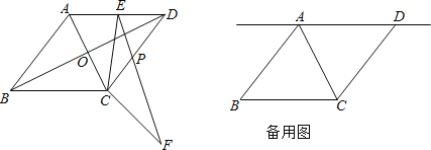
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,已知AC=2![]() ,AB=5.
,AB=5.
(1)求BD的长;
(2)点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),EF交CD于点P.
①当E为AD的中点时,求EF的长;
②连接AF、DF,当DF的长度最小时,求△ACF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
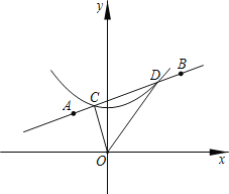
【题目】如图,在平面直接坐标系中,将反比例函数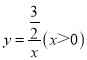 的图象绕坐标原点O逆时针旋转45°得到的曲线l,过点
的图象绕坐标原点O逆时针旋转45°得到的曲线l,过点![]() ,
,![]()
![]() 的直线与曲线l相交于点C、D,则sin∠COD=___ .
的直线与曲线l相交于点C、D,则sin∠COD=___ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com