
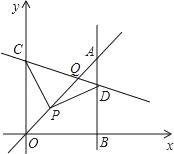
【题目】如图,平面直角坐标系中,已知P(1,1),C为y轴正半轴上一点,D为第一象限内一点,且PC=PD,∠CPD=90°,过点D作直线AB⊥x轴于B,直线AB与直线y=x交于点A,且BD=3AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为_____.
【答案】(![]() ,
,![]() )
)
【解析】
过P作MN⊥y轴,交y轴于M,交AB于N,过D作DH⊥y轴,交y轴于H,∠CMP=∠DNP=∠CPD=90°,求出∠MCP=∠DPN,证△MCP≌△NPD,推出DN=PM,PN=CM,设AD=a,求出DN=3a-1,得出3a-1=1,求出a=![]() ,得出D的坐标,在Rt△DNP中,由勾股定理求出PC=PD=
,得出D的坐标,在Rt△DNP中,由勾股定理求出PC=PD=![]() ,在Rt△MCP中,由勾股定理求出CM,得出C的坐标,设直线CD的解析式是y=kx+
,在Rt△MCP中,由勾股定理求出CM,得出C的坐标,设直线CD的解析式是y=kx+![]() ,把D(
,把D(![]() ,2)代入求出直线CD的解析式,解由两函数解析式组成的方程组,求出方程组的解即可.
,2)代入求出直线CD的解析式,解由两函数解析式组成的方程组,求出方程组的解即可.
过P作MN⊥y轴,交y轴于M,交AB于N,过D作DH⊥y轴,交y轴于H,
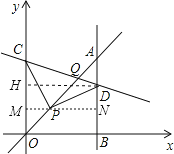
则∠CMP=∠DNP=∠CPD=90°,
∴∠MCP+∠CPM=90°,∠MPC+∠DPN=90°,
∴∠MCP=∠DPN,
∵P(1,1),
∴OM=BN=1,PM=1,
在△MCP和△NPD中,
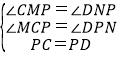 ,
,
∴△MCP≌△NPD(AAS),
∴DN=PM,PN=CM,
∵BD=3AD,
∴设AD=a,BD=3a,
∵P(1,1),
∴DN=3a-1,
则3a-1=1,
∴a=![]() ,即BD=2,
,即BD=2,
∵点A在直线y=x上,
∴AB=OB=![]() ,
,
在Rt△DNP中,由勾股定理得:PC=PD=![]() =
=![]() ,
,
在Rt△MCP中,由勾股定理得:CM=![]() =
=![]() ,
,
则C的坐标是(0,![]() ),
),
设直线CD的解析式是y=kx+![]() ,
,
把D(![]() ,2)代入得:k=-
,2)代入得:k=-![]() ,
,
即直线CD的解析式是y=-![]() x+
x+![]() ,
,
解方程组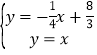 ,
,
得: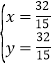 ,
,
即Q的坐标是(![]() ,
,![]() ),
),
故答案为:(![]() ,
,![]() ).
).


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.
(1)利用图中的条件,求反比例函数和一次函数的解析式.
(2)求△AOB的面积.
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
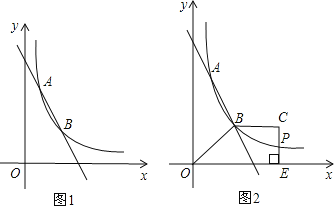
【题目】如图1,直线y=k1x+b与反比例函数y=![]() 的图象交于A(1,6),B(a,3)两点.
的图象交于A(1,6),B(a,3)两点.
(1)求k1、k2的值;
(2)结合图形,在第一象限内,直接写出k1x+b﹣![]() >0时,x的取值范围;
>0时,x的取值范围;
(3)如图2,梯形OBCE中,BC∥OE,过点C作CE⊥x轴于点E,CE和反比例函数的图象交于点P,当梯形OBCE的面积为9时,请判断PC和PE的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图(两图都不完整),下列结论错误的是( )

A. 该班总人数为50人B. 步行人数为30人
C. 乘车人数是骑车人数的2.5倍D. 骑车人数占20%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机生产厂家根据其产品在市场上的销售情况,决定对原来以每部2000元出售的一款彩屏手机进行调价,并按新单价的八折优惠出售,结果每部手机仍可获得实际销售价的20%的利润(利润=销售价—成本价).已知该款手机每部成本价是原销售单价的60%.
(1)求调整后这款彩屏手机的新单价是每部多少元?让利后的实际销售价是每部多少元?
(2)为使今年按新单价让利销售的利润不低于20万元,今年至少应销售这款彩屏手机多少部?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
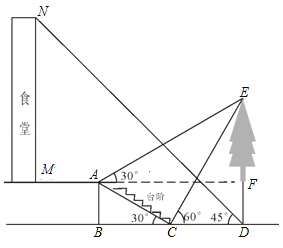
【题目】(2017湖北省鄂州市)小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B、C、D三点在同一直线上.
(1)求树DE的高度;
(2)求食堂MN的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

查看答案和解析>>
科目:初中数学 来源: 题型:
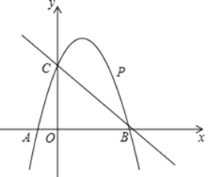
【题目】如图,已知二次函数y=ax2+bx+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0),AB=4.
(1)求二次函数y=ax2+bx+c的表达式;
(2)点M是二次函数对称轴上一动点,当点M运动到什么位置时,△ACM的周长最小?求出此时M点的坐标;
(3)点P是直线BC上方的抛物线上一动点,当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com