

分析 根据前四个图形的变化寻找旋转规律,得到△2015的直角顶点的坐标.
解答 解:由图可知,每3个三角形为一个循环组依次循环,
∵2015÷3=671余2,
∴△2015的直角顶点是第672组的第二个三角形的直角顶点,
∵A(-3,0),B(0,4),
∴OA=3,OB=4,
由勾股定理得,AB=$\sqrt{O{A}^{2}+O{B}^{2}}=\sqrt{{3}^{2}+{4}^{2}}$=5,
∴其纵坐标是$\frac{3×4}{5}=\frac{12}{5}$.
故答案为:$\frac{12}{5}$.
点评 本题考查了坐标与图形变化-旋转,观察图象得到每3个三角形为一个循环组依次循环是解题的关键,要注意相邻循环组的两个三角形的直角顶点互相重合.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
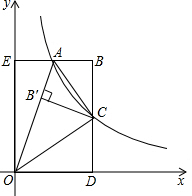 在平面直角坐标系中,点(0.5,4)在双曲线y=$\frac{m}{x}$上.
在平面直角坐标系中,点(0.5,4)在双曲线y=$\frac{m}{x}$上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,小岛P的周围20$\sqrt{2}$海里内有暗礁,某渔船沿北偏东60°的AM方向航行,在A处测得小岛P的方向为北偏东30°,且距A处40海里,该渔船若不改变航向,有无触礁的可能?若有可能触礁,则该渔船在A处应再向北偏东至少偏离多大角度才能脱险?
如图所示,小岛P的周围20$\sqrt{2}$海里内有暗礁,某渔船沿北偏东60°的AM方向航行,在A处测得小岛P的方向为北偏东30°,且距A处40海里,该渔船若不改变航向,有无触礁的可能?若有可能触礁,则该渔船在A处应再向北偏东至少偏离多大角度才能脱险?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com