
【题目】在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1,旋转角为θ(0°<θ<90°),连接AC1、BD1,AC1与BD1交于点P.
(1)如图1,若四边形ABCD是正方形.
①求证:△AOC1≌△BOD1.
②请直接写出AC1 与BD1的位置关系.
(2)如图2,若四边形ABCD是菱形,AC=6,BD=8,设AC1=kBD1.判断AC1与BD1的位置关系,说明理由,并求出k的值.
(3)如图3,若四边形ABCD是平行四边形,AC=6,BD=12,连接DD1,设AC1=kBD1.直接写出k的值和AC12+(kDD1)2的值.

【答案】(1)①证明见试题解析;②垂直;(2)AC1⊥BD1, ![]() ;(3)25.
;(3)25.
【解析】试题分析:(1)①如图1,根据正方形的性质得OC=OA=OD=OB,AC⊥BD,则∠AOB=∠COD=90°,再根据旋转的性质得OC1=OC,OD1=OD,∠COC1=∠DOD1,则OC1=OD1,利用等角的补角相等得∠AOC1=∠BOD1,然后根据“SAS”可证明△AOC1≌△BOD1;
②由∠AOB=90°,则∠OAB+∠ABP+∠OBD1=90°,所以∠OAB+∠ABP+∠OAC1=90°,则∠APB=90°所以AC1⊥BD1;
(2)如图2,根据菱形的性质得OC=OA=![]() AC,OD=OB=
AC,OD=OB=![]() BD,AC⊥BD,则∠AOB=∠COD=90°,再根据旋转的性质得OC1=OC,OD1=OD,∠COC1=∠DOD1,则OC1=OA,OD1=OB,利用等角的补角相等得∠AOC1=∠BOD1,加上
BD,AC⊥BD,则∠AOB=∠COD=90°,再根据旋转的性质得OC1=OC,OD1=OD,∠COC1=∠DOD1,则OC1=OA,OD1=OB,利用等角的补角相等得∠AOC1=∠BOD1,加上![]() ,根据相似三角形的判定方法得到△AOC1∽△BOD1,得到∠OAC1=∠OBD1,由∠AOB=90°得∠OAB+∠ABP+∠OBD1=90°,则∠OAB+∠ABP+∠OAC1=90°,则∠APB=90°,所以AC1⊥BD1;然后根据相似比得到
,根据相似三角形的判定方法得到△AOC1∽△BOD1,得到∠OAC1=∠OBD1,由∠AOB=90°得∠OAB+∠ABP+∠OBD1=90°,则∠OAB+∠ABP+∠OAC1=90°,则∠APB=90°,所以AC1⊥BD1;然后根据相似比得到![]() ,所以
,所以![]() ;
;
(3)与(2)一样可证明△AOC1∽△BOD1,则![]() ,所以
,所以![]() ;根据旋转的性质得OD1=OD,根据平行四边形的性质得OD=OB,则OD1=OB=OD,于是可判断△BDD1为直角三角形,根据勾股定理得
;根据旋转的性质得OD1=OD,根据平行四边形的性质得OD=OB,则OD1=OB=OD,于是可判断△BDD1为直角三角形,根据勾股定理得![]() ,所以
,所以![]() ,于是有
,于是有![]() .
.
试题解析:(1)①如图1,∵四边形ABCD是正方形,∴OC=OA=OD=OB,AC⊥BD,∴∠AOB=∠COD=90°,∵△COD绕点O按逆时针方向旋转得到△C1OD1,∴OC1=OC,OD1=OD,∠COC1=∠DOD1,∴OC1=OD1,∠AOC1=∠BOD1=90°+∠AOD1,在△AOC1和△BOD1中,∵OA=OB, ![]() ,
, ![]() ,∴△AOC1≌△BOD1;
,∴△AOC1≌△BOD1;
②AC1⊥BD1;
(2)AC1⊥BD1.理由如下:如图2,∵四边形ABCD是菱形,∴OC=OA=![]() AC,OD=OB=
AC,OD=OB=![]() BD,AC⊥BD,∴∠AOB=∠COD=90°,∵△COD绕点O按逆时针方向旋转得到△C1OD1,∴OC1=OC,OD1=OD,∠COC1=∠DOD1,∴OC1=OA,OD1=OB,∠AOC1=∠BOD1,∴
BD,AC⊥BD,∴∠AOB=∠COD=90°,∵△COD绕点O按逆时针方向旋转得到△C1OD1,∴OC1=OC,OD1=OD,∠COC1=∠DOD1,∴OC1=OA,OD1=OB,∠AOC1=∠BOD1,∴![]() ,∴△AOC1∽△BOD1,∴∠OAC1=∠OBD1,又∵∠AOB=90°,∴∠OAB+∠ABP+∠OBD1=90°,∴∠OAB+∠ABP+∠OAC1=90°,∴∠APB=90°,∴AC1⊥BD1;∵△AOC1∽△BOD1,∴
,∴△AOC1∽△BOD1,∴∠OAC1=∠OBD1,又∵∠AOB=90°,∴∠OAB+∠ABP+∠OBD1=90°,∴∠OAB+∠ABP+∠OAC1=90°,∴∠APB=90°,∴AC1⊥BD1;∵△AOC1∽△BOD1,∴ ,∴
,∴![]() ;
;
(3)如图3,与(2)一样可证明△AOC1∽△BOD1,∴![]() ,∴
,∴![]() ;∵△COD绕点O按逆时针方向旋转得到△C1OD1,∴OD1=OD,而OD=OB,∴OD1=OB=OD,∴△BDD1为直角三角形,在Rt△BDD1中,
;∵△COD绕点O按逆时针方向旋转得到△C1OD1,∴OD1=OD,而OD=OB,∴OD1=OB=OD,∴△BDD1为直角三角形,在Rt△BDD1中, ![]() ,∴
,∴![]() ,∴
,∴![]() .
.





科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
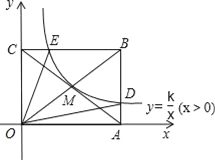
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边为( )
A. 3cm B. 7cm C. 7cm或3cm D. 7cm或5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
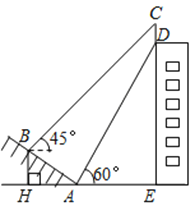
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1: ![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1: ![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程kx2﹣(3k﹣1)x+2(k﹣1)=0
(1)求证:无论k为任何实数,方程总有实数根;
(2)若此方程有两个实数根x1,x2,且|x1﹣x2|=2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
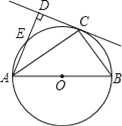
【题目】如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
(1)求证:AC平分∠BAD;
(2)若CD=3,AC=3![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com