练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．（1）计算：|-2|-（π-3.14）0；
    （2）解方程：$\frac{x+3}{2x-4}$=$\frac{3}{4}$．

    分析 （1）原式利用零指数幂法则，以及绝对值的代数意义化简，计算即可得到结果；
    （2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

    解答 解：（1）原式=2-1=1；
    （2）去分母得：4x+12=6x-12，
    移项合并得：x=12，
    经检验x=12是原方程的解．

    点评 此题考查了解分式方程，以及零指数幂，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

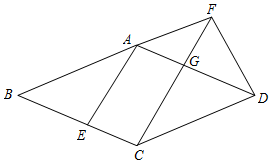    18．已知：如图，在菱形ABCD中，点E在边BC上，点F在BA的延长线上，BE=AF，CF∥AE，CF与边AD相交于点G．
    求证：（1）FD=CG；
    （2）CG2=FG•FC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．已知一次函数y=ax+5和y=bx+3，若a＞0且b＜0，则这两个一次函数的图象的交点在（　　）
    A．第四象限B．第三象限C．第二象限D．第一象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．解方程：$\frac{1-x}{x-2}$+1=$\frac{x}{2x-4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．（1）计算：（-2）2+2tan45°+（π-3.14）0；
    （2）解方程：$\frac{x}{x-3}$+$\frac{1}{3-x}$=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

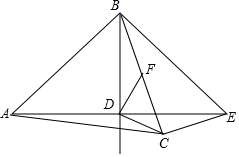    13．如图，在△ABC中，AB=AC，点D是△ABC内一点，AD=BD，且AD⊥BD，连接CD．过点C作CE⊥BC交AD的延长线于点 E，连接BE．过点D作DF⊥CD交BC于点F．
    （1）若BD=DE=$\sqrt{5}$，CE=$\sqrt{2}$，求BC的长；
    （2）若BD=DE，求证：BF=CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．2sin60°+（-$\frac{1}{2}$）-1-20160-|1-$\sqrt{3}$|

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，在⊙O中，∠OAB=45°，圆心O到弦AB的距离OE=2cm，则弦AB的长为（　　）
    A．2 cmB．3 cmC．4D．4 cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，用细线悬挂一个小球，小球在竖直平面内的A、C两点间来回摆动，A点与地面距离AN=14cm，小球在最低点B时，与地面距离BM=5cm，∠AOB=66°，求细线OB的长度．（参考数据：sin66°≈0.91，cos66°≈0.40，tan66°≈2.25）

    查看答案和解析>>

    同步练习册答案