
【题目】定义:对于一个数x,我们把[x]称作x的相伴数;若x≥0,则[x]=x﹣1;若x<0,则[x]=x+1.例:[0.5]=﹣0.5.
(1)求[![]() ]、[﹣1]的值;
]、[﹣1]的值;
(2)当a>0,b<0时,有[a]=[b],试求代数式(b﹣a)3﹣3a+3b的值;
(3)解方程:[x]+[x+2]=1.
 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】已知关于a的方程2(a﹣2)=a+4的解也是关于x的方程2(x﹣3)﹣b=7的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使![]() =b,点Q为PB的中点,请画出图形并求出线段AQ的长.
=b,点Q为PB的中点,请画出图形并求出线段AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
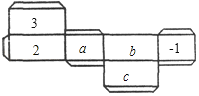
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.
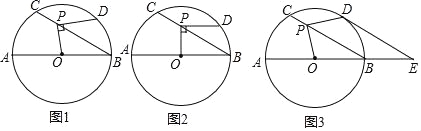
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当![]() 时,延长AB至点E,使BE=
时,延长AB至点E,使BE=![]() AB,连接DE.
AB,连接DE.
①求证:DE是⊙O的切线;
②求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上的A、B两点所对应的数分别为a、b.P为数轴上的一个动点.其中a,b满足(a﹣1)2+|b+5|=0,
(1)若点P为AB的中点,求P点对应的数.
(2)若点P从A点出发,以每秒2个单位的速度向左运动,t秒后,求P点所对应的数以及PB的距离.
(3)若数轴上点M、N所对应的数为m、n,其中A为PM的中点,B为PN的中点,无论点P在何处,![]() 是否为一个定值?若是,求出定值:若不是,请说明理由.
是否为一个定值?若是,求出定值:若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】O为直线AB上的一点,OC⊥OD,射线OE平分∠AOD.
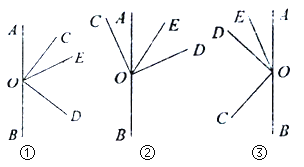
(1)如图①,判断∠COE和∠BOD之间的数量关系,并说明理由;
(2)若将∠COD绕点O旋转至图②的位置,试问(1)中∠COE和∠BOD之间的数量关系是否发生变化?并说明理由;
(3)若将∠COD绕点O旋转至图③的位置,探究∠COE和∠BOD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
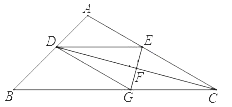
【题目】如图,△ABC中,CD平分∠ACB,CD的垂直平分线分别交AC、DC、BC
于点E、F、G,连接DE、DG.
(1)求证:四边形DGCE是菱形;
(2)若∠ACB=30°,∠B=45°,CG=10,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
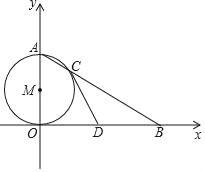
【题目】如图,OA是⊙M的直径,点B在x轴上,连接AB交⊙M于点C.
(1)若点A的坐标为(0,2),∠ABO=30°,求点B的坐标.
(2)若D为OB的中点,求证:直线CD是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com