
����Ŀ����ͼ������ΪP��2����4���Ķ��κ���y��ax2+bx+c��ͼ��ԭ�㣬��A��m��n���ڸú���ͼ���ϣ�����AP��OP��
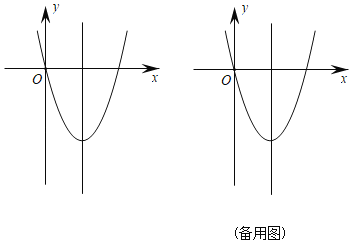
��1������κ���y��ax2+bx+c�ı���ʽ��
��2������APO��90�㣬���A�����ꣻ
��3������A���������ߵĶԳ���ĶԳƵ�ΪC����A����y��ĶԳƵ�ΪD������������x�����һ����ΪB�������������⣺
����m��4ʱ�����ж��ı���OBCD����״��˵�����ɣ�
����n��0ʱ�����ı���OBCD�����Ϊ12�����A�����꣮
���𰸡���1��y��x2��4x����2��A��![]() ����
����![]() ������3����ƽ���ı��Σ����ɼ���������A��1����3����A��3����3����
������3����ƽ���ı��Σ����ɼ���������A��1����3����A��3����3����
��������
��1������֪�ɵ���������x����һ�����㣨4��0��������2����4������4��0������0��0������y��ax2+bx+c���������ʽ��
��2���ɡ�APO��90�㣬��֪AP��PO������m��2��![]() ��������A��
��������A��![]() ����
����![]() ����
����
��3��������֪�ɵ�C��4��m��n����D����m��n����B��4��0�����ɵ�CD��OB��CD��CB�������ı���OBCD��ƽ���ı��Σ�
���ı�����OBCD��ƽ���ı��Σ�![]() ������12��4������n�����������A��1����3����A��3����3����
������12��4������n�����������A��1����3����A��3����3����
�⣺��1����ͼ��ԭ�㣬
��c��0��
�߶���ΪP��2����4��
����������x����һ�����㣨4��0����
����2����4���ͣ�4��0������y��ax2+bx��
��a��1��b����4��
����κ����Ľ���ʽΪy��x2��4x��
��2���ߡ�APO��90�㣬
��AP��PO��
��A��m��m2��4m����
��m��2��![]() ��
��
��m��![]() ��
��
��A��![]() ����
����![]() ����
����
��3��������֪�ɵ�C��4��m��n����D����m��n����B��4��0����
��CD��OB��
��CD��4��OB��4��
���ı���OBCD��ƽ���ı��Σ�
�����ı���OBCD��ƽ���ı��Σ�![]() ��
��
��12��4������n����
��n����3��
��A��1����3����A��3����3����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���BAC=75�����Ե�AΪ��ת���ģ�����ABC�Ƶ�A��ʱ����ת���á�AB'C'������BB'����BB'��AC'�����BAC�� �Ķ�����______________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ABC���������������ֱ�ΪA����3��5����B����4��3����C����1��1����д���������ԭ��ĶԳƵ������_____��_____��_____��
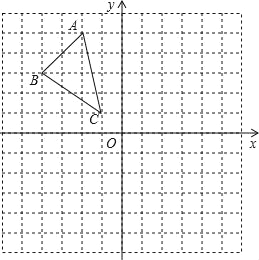
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
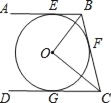
����Ŀ����ͼ��AB��BC��CD�ֱ����O������E��F��G���㣬��AB��CD��OB��6cm��OC��8cm��
������֤��OB��OC��
������CG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������Ա�μ����ѵ����ÿ�����10�Σ��ɼ��ֱ����£�
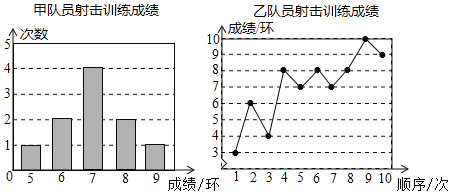
����������Ϣ�����������������£�
ƽ���ɼ�/�� | ��λ��/�� | ����/�� | ���� | |
�� | a | 7 | 7 | 1.2 |
�� | 7 | b | 8 | c |
��1��a��_____��b��_____��c��_____��
��2����գ�����������������������
�ٴ�ƽ��������λ���ĽǶ����Ƚϣ��ɼ��Ϻõ���_____��
�ڴ�ƽ�����������ĽǶ����Ƚϣ��ɼ��Ϻõ���_____��
�۳ɼ���Խ��ȶ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
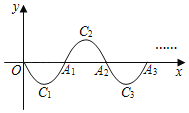
����Ŀ����ͼ�����κ���y��x��x��3����0��x��3����ͼ��ΪC1������x�ύ�ڵ�O��A1����C1��A1��ת180���C2����x���ڵ�A2����C2�Ƶ�A2��ת180���C3����x���ڵ�A3��������P��2020��m�������ͼ��������ת�������ͼ���ϣ���m��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��EF�����A����C����D����E�����������ϵ��( )
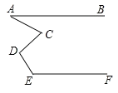
A. ��A����C����D����E��360��B. ��A����C����D����E��180��
C. ��E����C����D����A��90��D. ��A����D����C����E
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2+bx+c��a��0����x�ύ�ڵ�A����1��0������y��Ľ����ڣ�0��2������0��3��֮�䣨�����˵㣩����������Ϊ��1��n���������н��ۣ�
��4a+2b��0��
�ک�1��a��![]() ��
��
����������ʵ��m��a+b��am2+bm�ܳ�����
������x�ķ���ax2+bx+c��n��1����������ȵ�ʵ������
���н�����ȷ�ĸ���Ϊ��������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
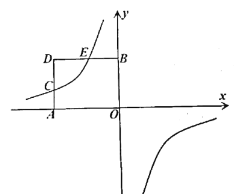
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����![]() �Ķ���
�Ķ���![]() ������
������![]() ��˫����
��˫����![]() �����
�����![]() �ı�
�ı�![]() ���ڵ�
���ڵ�![]() ��
��
(1)��˫����![]() �Ľ���ʽ�Լ���
�Ľ���ʽ�Լ���![]() �����ꣻ��
�����ꣻ��
(2)����![]() ��������
��������![]() �Ķ��㣻
�Ķ��㣻
�ٵ�˫����![]() ����
����![]() ʱ����
ʱ����![]() �����ꣻ
�����ꣻ
��ֱ��д����������![]() ����
����![]() ʱ���������������
ʱ���������������![]() ������ĸ����Լ���ʱ
������ĸ����Լ���ʱ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com