
【题目】已知,AB是半圆O的直径,弦CD∥AB,动点M、N分别在线段OC、CD上,AM的延长线与射线ON相交于点E,与弦CD相交于点F.
(1)如图1,若DN=OM,求证:AM=ON; 
(2)如图2,点P是弦CD上一点,若AP=OP,∠APO=90°,求∠COP的度数; 
(3)在(1)的条件下,若AB=20,cos∠AOC= ![]() ,当点E在ON的延长线上,且NE=NF时,求线段EF的长.
,当点E在ON的延长线上,且NE=NF时,求线段EF的长. 
【答案】
(1)解:如图1,
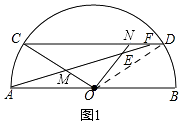
连接OD,
∴OA=OD,
∵CD∥AB,
∴∠BOD=∠NDO, ![]() ,
,
∴∠AOC=∠BCD,
∴∠AOC=∠CDO,
在△AMO和△OND中, 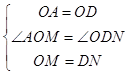 ,
,
∴△AMO≌△OND,
∴AM=ON,
(2)解:如图2,
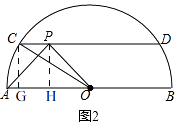
过点C作CG⊥AB,PH⊥AB,
∴CG=PH,
∵AP=OP,∠APO=90°,
∴∠AOP=45°,PH= ![]() OA,
OA,
∴CG= ![]() OA=
OA= ![]() OC,
OC,
∴∠AOC=30°,
∴∠COP=∠AOP﹣∠AOC=15°
(3)解:如图3,
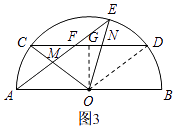
作OG⊥CD于G,连接OD,
∵AB=20,
∴OC=10
CG=OCcos∠C=OCcos∠AOC=10× ![]() =8
=8
∴CD=2CG=16
∵NE=NF,
∴∠E=∠EFN
∵CD∥AB,
∴∠EFN=∠A
∴∠E=∠A,
∴OE=OA
∵CD∥AB,
∴∠BOD=∠D=∠C=∠AOC
∴∠AOE=∠COD
∴△AOE≌△COD,
∴AE=CD=16
∵△AOM≌△ODN,
∴∠NOD=∠A=∠E
∴AE∥OD,
∴四边形AODF是平行四边形
∴AF=OD=10
∴EF=AE﹣AF=16﹣10=6
【解析】(1)先判断出∠BOD=∠NDO, ![]() 进而得出∠AOC=∠CDO,即可得出△AMO≌△OND,结论得证;(2)构造出直角三角形,先判断出PH=
进而得出∠AOC=∠CDO,即可得出△AMO≌△OND,结论得证;(2)构造出直角三角形,先判断出PH= ![]() OA,即可得出CG=
OA,即可得出CG= ![]() OC,进而求出∠AOC=30°,最后用角的差,即可得出结论.(3)先求出CD=2CG=16,再判断出△AOE≌△COD,进而判断出四边形AODF是平行四边形,最后用线段的差即可得出结论;
OC,进而求出∠AOC=30°,最后用角的差,即可得出结论.(3)先求出CD=2CG=16,再判断出△AOE≌△COD,进而判断出四边形AODF是平行四边形,最后用线段的差即可得出结论;


科目:初中数学 来源: 题型:
【题目】某服装店销售一批衬衣,每件进价250元,开始以每件400元的价格销售,每星期能卖出20件,后来因库存积压,决定降价销售,经过两次降价后每件售价为324元,求每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知直线AC的函数解析式为y= ![]() x+8,点P从点A开始沿AO方向以1个单位/秒的速度运动,点Q从O点开始沿OC方向以2个单位/秒的速度运动.如果P、Q两点分别从点A、点O同时出发,经过多少秒后能使△POQ的面积为8个平方单位?
x+8,点P从点A开始沿AO方向以1个单位/秒的速度运动,点Q从O点开始沿OC方向以2个单位/秒的速度运动.如果P、Q两点分别从点A、点O同时出发,经过多少秒后能使△POQ的面积为8个平方单位? 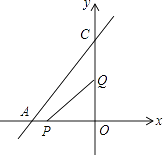
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京奥运会期间,某旅行社组团去北京观看某场足球比赛,入住某宾馆.已知该宾馆一楼房间比二楼房间少5间,该旅游团有48人,若全部安排在一楼,每间住4人,房间不够,每间住5人,有房间没住满.若全部安排在二楼,每间住3人,房间不够,每间住4人,则有房间没住满.你能根据以上信息确定宾馆一楼有多少房间吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果运回,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)如何安排甲、乙两种货车可一次性地运到?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果商场应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用点A(3,1)表示放置3个胡萝卜、1棵青菜,点B(2,3)表示放置2个胡萝卜、3棵青菜.

(1)写出其他各点C,D,E,F所表示的意义;
(2)若一只兔子从A到达B(顺着方格线走),有以下几条路可以选择:①A→C→D→B;②A→F→D→B;③A→F→E→B.则走哪条路吃到的胡萝卜最多?走哪条路吃到的青菜最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程的解正确的是( )
A. x-3=1的解是x=-2 B. ![]() x-2x=6的解是x=-4
x-2x=6的解是x=-4
C. 3x-4=![]() (x-3)的解是x=3 D. -
(x-3)的解是x=3 D. -![]() x=2的解是x=-
x=2的解是x=-![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com