练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】为弘扬“敬老爱老”传统美德，某校八年级（1）班的学生要去距离学校10km的敬老院看望老人，一部分学生骑自行车先走，过了20min后，其余学生乘汽车出发，结果乘汽车的同学早到10min．已知汽车的速度是骑车学生的4倍，求骑车学生的速度．

    【答案】15km/h

    【解析】试题分析：设骑车学生的速度为xkm/h，则汽车的速度为4xkm/h，根据一部分学生骑自行车先走，过了20min后，其余同学乘汽车出发，结果乘汽车的同学早到10min可列方程求解．

    试题解析：

    设骑车学生的速度为xkm/h，则汽车的速度为4xkm/h．依据题意得

    ﹣=+

    解得：x=15．

    检验：x=15时，12x≠0．所以原分式方程的解为x=15．

    并且此解符合题意．

    答：骑车学生的速度为15km/h．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若方程组 的解x，y满足0＜x+y＜1，则k的取值范围是（ ）
    A.﹣4＜k＜0
    B.﹣1＜k＜0
    C.0＜k＜8
    D.k＞﹣4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算。
    （1）解方程： +3=
    （2）解不等式：2x﹣3≤ （x+2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，小红将一张直角梯形纸片沿虚线剪开，得到矩形和三角形两张纸片，测得AB=15，AD=12．在进行如下操作时遇到了下面的几个问题，请你帮助解决．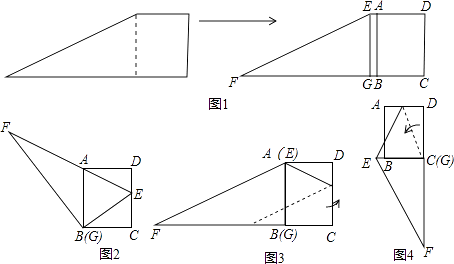

    （1）将△EFG的顶点G移到矩形的顶点B处，再将三角形绕点B顺时针旋转使E点落在CD边上，此时，EF恰好经过点A（如图2）求FB的长度；
    （2）在（1）的条件下，小红想用△EFG包裹矩形ABCD，她想了两种包裹的方法如图3、图4，请问哪种包裹纸片的方法使得未包裹住的面积大？（纸片厚度忽略不计）请你通过计算说服小红．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知A点坐标为（5，0），直线y=x+b（b＞0）与y轴交于点B，连接AB，∠α=75°，则b的值为（ ）
    A.3
    B.
    C.4
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABD，△ACE都是等边三角形，

    （1）求证：△ABE≌△ADC；

    （2）若∠ACD=15°，求∠AEB的度数；

    （3）如图2，当△ABD与△ACE的位置发生变化，使C、E、D三点在一条直线上，求证：AC∥BE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABD，△ACE都是等边三角形，

    （1）求证：△ABE≌△ADC；

    （2）若∠ACD=15°，求∠AEB的度数；

    （3）如图2，当△ABD与△ACE的位置发生变化，使C、E、D三点在一条直线上，求证：AC∥BE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一艘巡逻艇航行至海面B处时，得知正北方向上距B处20海里的C处有一渔船发生故障，就立即指挥港口A处的救援艇前往C处营救．已知C处位于A处的北偏东45°的方向上，港口A位于B的北偏西30°的方向上．求A、C之间的距离．（结果精确到0.1海里，参考数据 ≈1.41， ≈1.73）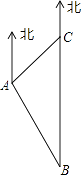

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=ax2+bx+c经过A（﹣1，0）、B（3，0）、C（0，3）三点，直线l是抛物线的对称轴．

    （1）求抛物线的函数关系式；
    （2）设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；
    （3）在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．
    （4）问：若抛物线顶点为D，点Q为直线AC上一动点，当△DOQ的周长最小时，求点Q的坐标

    查看答案和解析>>

    同步练习册答案