
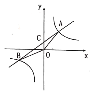
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() =______,
=______,![]() =______;
=______;
(2)根据函数图象可知,当![]() 时,
时,![]() 的取值范围是____________.
的取值范围是____________.
(3)求![]()
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 12.
12.
【解析】
(1)由A与B为一次函数与反比例函数的交点,将B坐标代入反比例函数解析式中,求出k2的值,确定出反比例解析式,将B坐标代入一次函数解析式中即可求出k1的值;
(2)将A的坐标代入反比例解析式中求出m的值,确定出A的坐标,由图象找出一次函数图象在反比例函数图象上方时x的范围即可;
(3)利用三角形的面积公式,根据S△AOB=S△AOC+S△BO即可求出三角形AOB的面积.
解:(1) )∵一次函数y1=k1x+2与反比例函数y2=![]() 的图象交于点A(4,m)和B(-8,-2),
的图象交于点A(4,m)和B(-8,-2),
∴k2=(-8)×(-2)=16,-2=-8k1+2,
∴k1=![]() ;
;
故答案为:![]() ,
,![]() ;
;
(2) 将A(4,m)代入y=![]() 得,m=
得,m=![]() =4,
=4,
∴A(4,4),
∵一次函数y1=k1x+2与反比例函数y2=![]() 的图象交于点A(4,4)和B(-8,-2),
的图象交于点A(4,4)和B(-8,-2),
∴当y1>y2时,x的取值范围是-8<x<0或x>4,
故答案为:![]() 或
或![]() ;
;
(3)由(1)知,![]() ,
,![]() ,
,![]() ,
,
点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标为
的坐标为![]()
![]() ,
,
![]() =12.
=12.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】王先生到泉州台商投资区行政服务中心大楼办事,假定乘电梯向上一楼记作+1,向下一楼记作﹣1,王先生从1楼出发,电梯上下楼层依次记录如下:(单位:层)
+6,﹣3,+10,﹣8,+12,﹣7,﹣10.
(1)请你通过计算说明王先生最后是否回到出发点1楼.
(2)该中心大楼每层高3m,电梯每向上或下1m需要耗电0.1度,根据王先生现在所处位置,请你算算,他办事时电梯需要耗电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陆老师去水果批发市场采购苹果,他看中了A,B两家苹果,这两家苹果品质一样,零售价都我6元/千克,批发价各不相同.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
数量范围(千克) | 0~500部分 | 500以上~1500 | 1500以上~2500部分 | 2500以上部分 |
价格补贴 | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(1)如果他批发700千克苹果,则他在A、B两家批发分别需要多少元?
(2)如果他批发x千克苹果(1500<x<2000),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)A、B两店在互相竞争中开始了互怼,B说A店的苹果总价有不合理的,有时候买的少反而贵,忽悠消费者;A说B的总价计算太麻烦,把消费者都弄糊涂了;旁边陆老师听完,提出两个问题希望同学们帮忙解决:
问题1:能否举例说明A店买的多反而便宜?
问题2:B店老板比较聪明,在平时工作中发现有巧妙的方法:总价=购买数量×单价+价格补贴;
注:不同的单价,补贴价格也不同;只需提前算好即可填下表:
数量范围(千克) | 0~500部分 | 500以上~1500 | 1500以上~2500 | 2500以上部分 |
价格补贴 | 0元 | 300 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点P在函数![]() (x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )
(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )
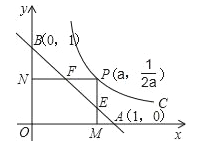
A. 4 B. 2 C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,连接DP,将直线DP绕点P顺时针旋转使∠DPG=∠DAC,且过D作DG⊥PG,连接CG,则CG最小值为( )
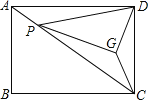
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动,2秒后,两点相距16个单位长度,已知动点A、B的速度比为1:3(速度单位:1个单位长度秒).
![]()
(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,满足OB=2OA?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠1=60°,下列结论错误的是( )
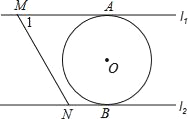
A. MN=![]() B. 若MN与⊙O相切,则AM=
B. 若MN与⊙O相切,则AM=![]()
C. l1和l2的距离为2 D. 若∠MON=90°,则MN与⊙O相切
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com