
【题目】已知:△ABC内接于⊙O,连接CO并延长交AB于点E,交⊙O于点D,满足∠BEC=3∠ACD.
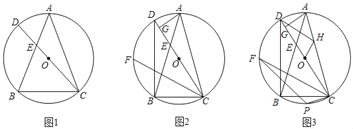
(1)如图1,求证:AB=AC;
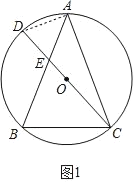
(2)如图2,连接BD,点F为弧BD上一点,连接CF,弧CF=弧BD,过点A作AG⊥CD,垂足为点G,求证:CF+DG=CG;
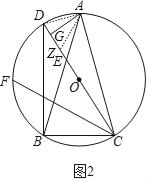
(3)如图3,在(2)的条件下,点H为AC上一点,分别连接DH,OH,OH⊥DH,过点C作CP⊥AC,交⊙O于点P,OH:CP=1:![]() ,CF=12,连接PF,求PF的长.
,CF=12,连接PF,求PF的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接AD.设∠BEC=3α,∠ACD=α,利用等量代换得出∠ABC=∠ACB,最后进一步证明结论即可;
(2)连接AD,在CD上取一点Z,使得CZ=BD,通过证明△ADB≌△AZC得出AD=AZ,然后进一步证明即可;
(3)连接AD,PA,作OK⊥AC于K,OR⊥PC于R,CT⊥FP交FP的延长线于T,利用三角函数以及勾股定理进一步求解即可.
(1)证明:如图1中,连接AD.设∠BEC=3α,∠ACD=α.
∵∠BEC=∠BAC+∠ACD,
∴∠BAC=2α,
∵CD是直径,
∴∠DAC=90°,
∴∠D=90°﹣α,
∴∠B=∠D=90°﹣α,
∵∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣2α﹣(90°﹣α)=90°﹣α.
∴∠ABC=∠ACB,
∴AB=AC;
(2)证明:如图2中,连接AD,在CD上取一点Z,使得CZ=BD.
∵弧BD=弧CF,
∴DB=CF,
∵∠DBA=∠DCA,CZ=BD,AB=AC,
∴△ADB≌△AZC(SAS),
∴AD=AZ,
∵AG⊥DZ,
∴DG=GZ,
∴CG=CZ+GZ=BD+DG=CF+DG.
(3)连接AD,PA,作OK⊥AC于K,OR⊥PC于R,CT⊥FP交FP的延长线于T.
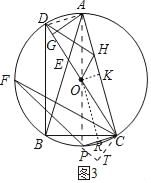
∵CP⊥AC,
∴∠ACP=90°,
∴PA是直径,
∵OR⊥PC,OK⊥AC,
∴PR=RC,∠ORC=∠OKC=∠ACP=90°,
∴四边形OKCR是矩形,
∴RC=OK,
∵OH:PC=1:![]() ,
,
∴设OH=![]() a,PC=2a,
a,PC=2a,
∴PR=RC=a,
∴RC=OK=a,sin∠OHK=![]() ,
,
∴∠OHK=45°,
∵OH⊥DH,
∴∠DHO=90°,
∴∠DHA=180°﹣90°﹣45°=45°,
∵CD是直径,
∴∠DAC=90°,
∴∠ADH=90°﹣45°=45°,
∴∠DHA=∠ADH,
∴AD=AH,
∵∠COP=∠AOD,
∴AD=PC,
∴AH=AD=PC=2a,
∴AK=AH+HK=2a+a=3a,
在Rt△AOK中,tan∠OAK=![]() ,OA=
,OA=![]() =
=![]() ,
,
∴sin∠OAK=![]() ,
,
∵∠ADG+∠DAG=90°,∠ACD+∠ADG=90°,
∴∠DAG=∠ACD,
∵AO=CO,
∴∠OAK=∠ACO,
∴∠DAG=∠ACO=∠OAK,
∴tan∠ACD=tan∠DAG=tan∠OAK=![]() ,
,
∴AG=3DG,CG=3AG,
∴CG=9DG,
由(2)可知,CG=DG+CF,
∴DG+12=9DG,
∴DG=![]() ,AG=3DG=3×
,AG=3DG=3×![]() =
=![]() ,
,
∴AD=![]() ,
,
∴PC=AD=![]() ,
,
∵sin∠F=sin∠OAK,
∴sin∠F=![]() ,
,
∴CT=![]() =
=![]() ×12=
×12=![]() ,FT=
,FT=![]() ,PT=
,PT=![]() ,
,
∴PF=FT﹣PT=![]() ﹣
﹣![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,下列结论中不正确的是. ( )
,下列结论中不正确的是. ( )
A.图象必经过点(3,-2)B.图象位于第二、四象限
C.若![]() ,则
,则![]() D.在每一个象限内,
D.在每一个象限内, ![]() 随
随![]() 值的增大而增大
值的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】样本一:92,94,96;样本二:m,94,96.嘉淇通过相关计算并比较,发现:样本二的平均数较大,方差较小.则m的值可能是( )
A.91B.92C.95D.98
查看答案和解析>>
科目:初中数学 来源: 题型:
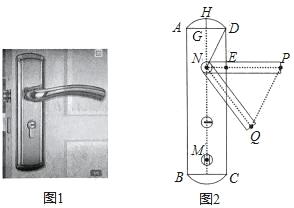
【题目】小明家的门框上装有一把防盗门锁(如图1).其平面结构图如图2所示,锁身可以看成由两条等弧AD,弧BC和矩形ABCD组成,弧BC的圆心是倒锁按钮点M.已知弧AD的弓形高GH=2cm,AD=8cm,EP=11cm.当锁柄PN绕着点N旋转至NQ位置时,门锁打开,此时直线PQ与弧BC所在的圆相切,且PQ∥DN,tan∠NQP=2.
(1)弧BC所在圆的半径为_____cm.
(2)线段AB的长度约为_____cm.(![]() ≈2.236,结果精确到0.1cm)
≈2.236,结果精确到0.1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为定值,E是边CD上的动点(不与点C,D重合),AE交对角线BD于点F,FG⊥AE交BC于点G,GH⊥BD于点H.现给出下列命题:①AF=FG;②FH的长度为定值.则( )
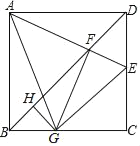
A.①是真命题,②是真命题B.①是真命题,②是假命题
C.①是假命题,②是真命题D.①是假命题,②是假命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图.请你根据统计图回答下列问题:
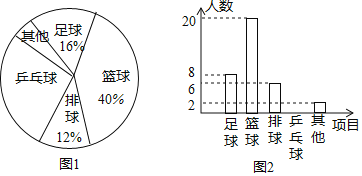
(1)请补全条形统计图(图2);
(2)在扇形统计图中,“篮球”部分所对应的圆心角是____________度?
(3)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
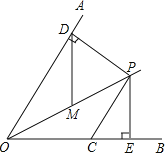
【题目】如图,已知OP平分∠AOB,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.CP=![]() ,PD=6.如果点M是OP的中点,则DM的长是_____.
,PD=6.如果点M是OP的中点,则DM的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张看上去无差别的卡片,上面分别写着1,2,3,4.
(1)一次性随机抽取2张卡片,求这两张卡片上的数字之和为奇数的概率;
(2)随机摸取1张后,放回并混在一起,再随机抽取1张,求两次取出的卡片上的数字之和等于4的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com